Codage des entiers naturels

Principe

En informatique, selon le besoin et le contexte, on a le choix d’écrire les nombres sous 4 représentations différentes :

  1. le décimal (→ base 10)

  2. le binaire (→ base 2)

  3. l'hexadécimal (→ base 16)

  4. l'octal (→ base 8)

Depuis l’antiquité, on écrit les nombres avec des symboles (chiffres, lettres, formes géométriques…​) qui, associés entre eux, peuvent représenter n’importe quelle valeur. Plusieurs représentations ont existé au cours de l’histoire mais celle qui a supplanté les autres est la représentation qui repose sur le principe de position.

Dans ce genre de représentation, la valeur du symbole utilisée pour écrire le nombre varie en fonction de la place — son rang — qu’il occupe dans l’écriture du nombre : c’est ce qu’on appelle son poids. Ex. : Dans le nombre 808, exprimé en décimal, le ‘8’ de gauche (→ colonne des centaines) et vaut/“pèse” donc 100 fois plus que le ‘8’ de droite (→ colonne des unités) même si ce sont les mêmes chiffres.

Le décimal, l’hexadécimal, le binaire et l’octal suivent ce principe de position en utilisant des bases différentes (respectivement 10, 16, 2 et 8). Ces représentations donneront à chaque symbole du nombre — chiffres mais aussi lettres pour l’hexadécimal — un poids différent.

Ainsi, quelle que soit la représentation choisie, la valeur d’un nombre pourra toujours être obtenue avec la formule suivante :

formule generale

avec :

  • b, la base associée à la représentation choisie (décimal → 10, binaire → 2, hexadécimal → 16, octal → 8)

  • ai, un des symboles définis pour la base :

    • décimal → [0, 1, 2, …​, 9]

    • binaire → [0, 1]

    • hexadécimal → [0, 1, 2, …​, 9, A, B, C ,D, E ,F]

    • octal → [0, 1, 2, …​, 7]

Voyons maintenant ça d’un peu plus près …​

Par la suite, pour lever toute ambiguité sur la représentation utilisée dans le texte pour écrire un nombre, on le fera suivre par un indice indiquant sa base (ou plus exactement le caractère ‘|’ suivi de sa base).

Exemples :

  • 48|10 → le nombre 48 en représentation décimale (4 x 101 + 8 x 100)

  • 21|16 → le nombre 33 en représentation hexadécimale (2 x 161+ 1 x 160)

  • 1100|2 → le nombre 12 en représentation binaire (1 x 23 + 1 x 22 ^+ 0 x 21 + 0 x 20)

Système décimal

C’est la représentation la plus répandue. On la maitrise plutôt bien puisqu’on l’utilise depuis qu’on est petits ! 😉

Chaque chiffre du nombre représente une puissance de 10.

Exemples :

  • 12|10 = 1 x 101 + 2 x 100 = 1 x 10 + 2 x 1

  • 123|10 = 1 x 102 + 2 x 101 + 3 x 100 = 1 x 100 + 2 x 10 + 3 x 1

100 vaut bien 1 et pas 0.

Pour écrire un nombre en base 10 dans des codes source C/C++ ou Python, il suffit de le saisir tel quel en veillant à ne pas le précéder d’un 0.

foobar.c
int main() {
    int i = 12; (1)
    int j = 012; // ⚠ (2)
}
1 on définit une variable i qui contient la valeur 12|10
2 on définit une variable j qui contient la valeur 10|10 et non pas la valeur 12|10 comme on pourrait le croire. Ceci est la conséquence du ‘0’ devant le ‘12’ qui indique, en langage C, que le nombre est exprimé en octal (→ voir pluys loin) et non en décimal.

Système binaire

C’est la représentation qui est souvent utilisée pour effectuer des calculs de sous-réseaux informatique et lorsqu’on programme proche du matériel (registres de microprocesseurs ou de composants périphériques).

Chaque symbole code une puissance de 2.

Exemples :

  • 101|2 = 1 x 22 + 0 x 21 + 1 x 20 = 1 x 4 + 0 x 2 + 1 x 1 = 5|10

  • 1010|2 = 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 = 1 x 8 + 0 x 4 + 1 x 2 + 0 x 1 = 10|10

Il est plutôt rare d’exprimer des nombres en binaire dans des codes source.

Ceci s’explique d’une part par le fait que c’est rarement pris en charge par les langages de programmation et d’autre part car c’est trop long à écrire.

le langage Python propose néanmoins la possibilité de saisir les nombres binaires en utilisant le préfixe 0b (zéro suivi de la lettre ‘b’).

foobar.py
if __name__ == '__main__':
        foo = 0b11000011 (1)
        print(f"{foo:b} en binaire vaut {foo:o} en octal, {foo:d} en décimal et {foo:x} en hexadécimal ") (2)
# Affiche :
# 11000011 en binaire vaut 303 en octal, 195 en décimal et c3 en hexadécimal
1 on définit une variable foo qui contient la valeur 195|10 (← 11000011|2)
2 on affiche le contenu de la variable foo en binaire ainsi que sa représentation en octal, décimal puis hexadécimal.

Bit, Quartet, Octet

Chaque symbole utilisé pour exprimer un nombre en binaire est appelé bit (Binary digIT) pour bien faire la distinction avec les chiffres ‘0’ et ‘1’ du système décimal.

Les nombres représentés en binaire comportent généralement un nombre de bits multiple de 8. En effet, au niveau interne, les composants électroniques mémorisent les nombres avec des séries de transistors dont l’état est soit passant soit bloqué à la manière d’un interrupteur. Ils sont généralement regroupés par 8 et la valeur codée par ces 8 bits est ce qu’on appelle un octet (ou un byte en anglais). En représentant les nombres binaires avec un nombre de bits multiple de 8 on se rapproche ainsi de la structure interne du composant électronique.

Selon le nombre de bits d’un nombre binaire on le qualifiera de :

  • Octet (Byte) lorsqu’il comporte 8 bits

  • Mot (Word) lorsqu’il comporte 16 bits

  • Double Mot (Double Word ou DWord) lorsqu’il comporte 32 bits

  • Quadruple Mot (Quad Word ou QWord) lorsqu’il comporte 64 bits

On est parfois amené à manipuler des suites de 4 bits : c’est ce qu’on appelle des quartets (ou nibbles en anglais).

MSB, LSB

Dans un nombre binaire, on se réfère souvent aux bits qui sont situés aux 2 extrémités.

Le bit le plus à gauche est souvent désigné par l’acronyme MSB pour Most Significant Bit (ou bit le plus significatif en français).

Le bit le plus à droite est, quant à lui, désigné par LSB pour Less Significant Bit (ou bit le moins significatif en français).

Tableau 1. Exemple pour le nombre 10100101|2
1 0 1 0 0 1 0 1

MSB

LSB

Multiples d’octets

Pour exprimer la capacité des différents supports de stockage (mémoire RAM, clé USB, disque SSD…​) ou les débits de données sur les réseaux, on utilise systématiquement des multiples de l’octet.

2 types de multiplicateurs sont utilisés :

  1. ceux correspondant à des puissances de 10 :

    • le kilooctet (ko) = 103 octets = 1000 octets

    • le mégaoctet (Mo) = 106 octets (million) = 1000 ko

    • le gigaoctet (Go) = 109 octets (milliard) = 1000 Mo = 106 ko

    • le téraoctet (To) = 1012 octets (billion) = 1000 Go = 106 Mo = 109 ko

    • le pétatoctet (Po) = 1015 octets (billiard) = 1000 To = 106 Go = 109 Mo = 1012 ko

  2. ceux correspondant à des puissances de 2

    • le kibioctet (Kio) = 210 octets = 1024 octets

    • le mébioctet (Mio) = 220 octets = 1024 Kio

    • le gibioctet (Gio) = 230 octets = 1024 Mio

    • le tébioctet (Tio) = 240 octets = 1024 Gio

    • …​

Application : La capacité d’un disque SSD est annoncée comme étant 512Go. Quelle est sa capacité en Gio et en Tio ?

Réponse

Capacité donnée : 512 Go = 512 . 109 octets

⇒ Capacité en Gio : 512 . 109 / 230 ≈ 476,84 Gio

⇒ Capacité en Tio : 512 . 109 / 240 ≈ 0,46 Tio

Système hexadécimal

Cette représentation est largement utilisée. On l’emploie pour représenter :

  • des valeurs binaires dans les codes source C/C++, Python, Javascript…​

  • les adresses matérielles (adresses MAC) des cartes réseau

  • des couleurs en HTML

  • …​

Chaque symbole d’un nombre représenté en hexadécimal (→ hex digit) correspond à une puissance de 16.

Dans cette représentation, 16 symboles sont nécessaires. Pour cela, on utilise les 10 chiffres (‘0’ à ‘9’) et les 6 premières lettres de l’alphabet (’A’ à ’F’) dont les valeurs en décimales correspondent aux nombres 10 à 15.

Exemples :

  • 3B|16 = 3|10 x 161 + 11|10 x 160 = 59|10

  • 1CF|16 = 1|10 x 162 + 12|10 x 161 + 15|10 x 160 = 463|10

Pour écrire un nombre en base 16 dans des codes source (C/C++ , Python, Javascript …​), il suffit de le saisir en le précédant du préfixe 0x (zéro suivi de la lettre ‘x’).

foobar.c
int main() {
    int i = 0x5A; (1)
}
1 on définit une variable i qui contient la valeur 5A|16 = 90|10

Système octal

Cette représentation est peu utilisée. On la rencontre essentiellement dans le système d’exploitation Linux pour coder les droits d’accès sur les fichiers.

Chaque symbole utilisé dans la représentation en octal d’un nombre (chiffres de ‘0’ à ‘7’ uniquement) représente une puissance de 8.

Exemples :

  • 62|8 = 6|10 x 81 + 2|10 x 80 = 50|10

  • 750|8 = 7|10 x 82 + 5|10 x 81 + 0|10 x 80 = 488|10

Pour écrire un nombre en base 8 dans des codes source C/C++, Javascript, PHP (v < 8.1), il suffit de le saisir en le précédant du chiffre ‘0’.

foobar.c
int main() {
    int i = 0750; (1)
}
1 on définit en C/C++une variable i qui contient la valeur 750|8 = 488|10

Dans Python 3.0+ et PHP v8.1+, une valeur octale sera préfixée de 0o (chiffre ‘0’ suivi de la lettre ‘o’).

foobar.py
if __name__ == '__main__':
        foo = 0o750 (1)
        print(f"{foo:o} en octal vaut {foo:d} en décimal, {foo:x} en hexadécimal et {foo:b} en binaire") (2)
# Affiche :
# 750 en octal vaut 488 en décimal, 1e8 en hexadécimal et 111101000 en binaire
1 on définit une variable foo qui contient la valeur 195|10 (← 11000011|2)
2 on affiche le contenu de la variable foo en octal ainsi que sa représentation en décimal, hexadécimal puis binaire.

Conversions entre bases

Il est impératif de savoir passer d’une base à l’autre.

Par exemple, il est impossible de calculer des masques de sous-réseau si on ne maitrise pas les conversions de la base 10 à la base 2.

Une autre situation dans laquelle une conversion est nécessaire est lorsqu’on désire saisir des nombres binaires dans un langage ne les prenant pas en charge au niveau du code source (Ex. : C++ dans sa version inférieure à C++14). On va alors plutôt utiliser la représentation hexadécimale pour exprimer ces nombres — plutôt que la décimale — car le passage du binaire à l’hexadécimal (ou inversement) est intuitif et très facile à réaliser.

Conversion binaire ⇆ décimal

Décimal → Binaire

Il existe plusieurs méthodes :

  1. L’utilisation d’un tableau de puisssances de 2

  2. Les soustractions successives

  3. Les divisions successives

► Le tableau de puissances de 2

C’est la méthode la plus rapide pour les petits nombres si on connait bien les puissances de 2 par cœur.

La méthode consiste à :

  1. créer un tableau de conversion avec les puissances successives de 2 à partir de la droite : 20, 21, 22, 23 …​

  2. prendre le nombre décimal à convertir

  3. parcourir le tableau de gauche à droite et :

    • inscrire un ‘1’ dans la colonne si le nombre est supérieur ou égale à la puissance de 2 de la colonne

    • inscrire un ‘0’ dans le cas contraire

  4. Soustraire la puissance de 2 de la colonne au nombre

  5. Répétez les étapes 3 et 4 avec le reste obtenu jusqu’à ce que toutes les colonnes soient traitées.

Exemple pour 156|10 qui donne 10011100|2 en binaire :

128 64 32 16 8 4 2 1

1

0

0

1

1

1

0

0

Explications :

  1. 156 ≥ 128 : On inscrit 1 dans la 8ème colonne et on calcule 156 - 128 = 28

  2. 28 < 64 : On inscrit 0 dans la 7ème colonne.

  3. 28 < 32 : On inscrit 0 dans la 6ème colonne.

  4. 28 ≥ 16 : On inscrit 1 dans la 5ème colonne et on calcule 28 - 16 = 12.

  5. 12 ≥ 8 : On inscrit 1 dans la 4ème colonne et on calcule 12 - 8 = 4.

  6. 4 ≥ 4 : On inscrit 1 dans la 3ème colonne et on calcule 4 - 4 = 0.

  7. 0 < 2 : On inscrit 0 dans la 2ème colonne.

  8. 0 < 1 : On inscrit 0 dans la 1ère colonne.

► Les soustractions successives

Cette méthode — applicable aux petits nombres — est considérée comme rapide et intuitive.

Elle consiste à :

  1. Déterminer la plus grande puissance de 2 inférieure ou égale au nombre décimal.

  2. Soustraire cette puissance de 2 du nombre décimal.

  3. Noter un 1 dans la position binaire correspondante.

  4. Répéter les étapes 1 à 3 avec le reste obtenu à l’étape 2, jusqu’à ce que le reste soit 0.

  5. Compléter avec des 0 les positions binaires non utilisées.

Exemple pour 35|10 qui donne 100011|2 en binaire:

  1. 35|10 est supérieur à 25(→32) mais inférieur à 26(→64)
    ⇒ On met un 1 au rang 5 dans le nombre binaire recherché et on complète à droite par des 0 : 100000|2

  2. On calcule le reste : 35 - 32 = 3

  3. 3|10 est est supérieur à 21(→2) mais inférieur à 22(→4)
    ⇒ On met un 1 au rang 1 dans le nombre binaire recherché : 100010|2

  4. On calcule le reste : 3 - 2 = 1

  5. 1|10 est compris entre 20(→1) et 21(→2)
    ⇒ On met un 1 au rang 0 dans le nombre binaire recherché : 100011|2

  6. On calcule le reste : 1 - 1 = 0
    Le reste vaut 0 donc on s’arrête.

Au final 35|10 donne 100011|2 en binaire

La puissance de 2 inférieure ou égale à un nombre N peut être obtenue :

  • soit mentalement par calcul des puissances de 2 successives (→ 20, 21, 22, …​) jusqu’à obtenir la plus grande qui soit inférieure au nombre à convertir

  • soit en prenant la partie entière du résultat de log(N) / log(2).

Exemple pour 192|10 :

  • 20=1≤192 → 21=2≤192 → 22=4≤192 → …​ → 27=128≤192 → 28=256>192

    ⇒ 7 est la puissance de 2 max. contenue dans 192

  • ⌊ log(192)/log(2) ⌋ = ⌊ 2,28/0,30 ⌋ = ⌊ 7,58 ⌋= 7

    On tombe sur le même résultat 🤩

► Les divisions successives

Cette méthode est la plus efficace pour les grands nombres.

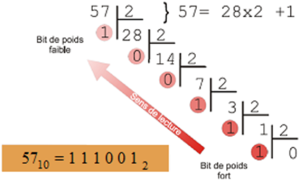
Elle consiste à effectuer la division entière du nombre à convertir jusqu’à ce que le quotient soit égal à 0. Les restes successifs des divisions — en partant du bas —  correspondent alors à la représentation binaire du nombre.

Exemple avec la valeur 57|10 qui donne 111001|2 en binaire :

dectobin

Binaire → Décimal

La méthode consiste à multiplier chaque bit à 1 du nombre binaire par son poids (← poids = 2rang_du_bit) et faire la somme de ces produits.

Exemple avec 111001|2 :

111001|2 = 1 x 25 + 1 x 24 + 1 x 23 + 1 x 20 = 32 + 16 + 8 + 1 = 57|10

Conversion binaire ⇆ hexadécimal

Binaire → Hexadécimal

La méthode consiste à :

  1. regrouper les bits par paquets de 4 en partant de la droite

  2. ajouter éventuellement des 0 à gauche pour avoir un nombre entier de paquets de 4 bits

  3. convertir chaque paquet en hexadécimal selon la table de correspondance suivante qu’il est fortement recommandé d’apprendre par cœur :

    Binaire

    →

    Hexadécimal

    Binaire

    →

    Hexadécimal

    0000

    →

    0

    1000

    →

    8

    0001

    →

    1

    1001

    →

    9

    0010

    →

    2

    1010

    →

    A

    0011

    →

    3

    1011

    →

    B

    0100

    →

    4

    1100

    →

    C

    0101

    →

    5

    1101

    →

    D

    0110

    →

    6

    1110

    →

    E

    0111

    →

    7

    1111

    →

    F

Exemples :

  • 11000000|2 ⇒ [1100|2][0000|2] ⇒ [C|16][0|16] ⇒ C0|16

  • 1110101100|2 ⇒ 11|2[1010|2][1011|2] ⇒ [0011|2][1010|2][1011|2] ⇒ [3|16][A|16][B|16] ⇒ 3AB|16

Hexadécimal → Binaire

Cette conversion s’obtient en remplaçant directement chaque symbole du nombre hexadécimal par son équivalent binaire sur 4 bits en utilisant la table de correspondance précédente.

Exemples :

  • 6C|16 ⇒ [6|16][C|16] ⇒ [0110|2][1100|2] ⇒ 01101100|2

  • A35|16 ⇒ [A|16][3|16][5|16] ⇒ [1010|2][0011|2][0101|2] ⇒ 10100110101|2

Conversion binaire ⇆ octal

Le principe de la conversion est le même que pour une conversion binaire ⇆ hexadécimal sauf que l’on fait des paquets de 3 bits au lieu de 4.

Binaire → Octal

Exemples :

  • 101011|2 ⇒ [101|2][011|2] ⇒ [5|8][3|8] ⇒ 53|8

  • 1011010|2 ⇒ 1|2[011|2][010|2] ⇒ [001|2][011|2][010|2] ⇒ [1|8][3|8][2|8] ⇒ 132|8

Octal → Binaire

Exemples :

  • 27|8 ⇒ [2|8][7|8] = [010|2][111|2] ⇒ 010111|2

  • 755|8 ⇒ [7|8][5|8][5|8] ⇒ [111|2][101|2][101|2] ⇒ 111101101|2

🞄  🞄  🞄