Python pour la science des données
S’il est un domaine dans lequel Python excelle c’est bien celui de la science des données (→ data science).
Ce document vise à vous familiariser avec l’utilisation de librairies de base de Python qui permettent de traiter de grands nombres de données et aussi de les représenter :
-
numpy -
matplotlib
Généralités
Voici comment Wikipedia définit la science des données :
La science des données est un domaine interdisciplinaire qui utilise les mathématiques, les statistiques, le calcul scientifique, les méthodes scientifiques, les process, les algorithmes et les systèmes informatiques automatisés pour extraire et extrapoler des connaissances à partir de grandes quantités de données brutes structurées ou non.
Elle est souvent associée aux données massives, à l’analyse des données, aux techniques d’apprentissage automatique comme le Machine Learning et le Deep Learning.
On voit donc que la science des données revêt beaucoup d’importance aujourd’hui puisqu’elle constitue le socle de l'intelligence artificielle.
Cette science des données va permettre d’élaborer des modèles visant à :
-
prendre des décisions à partir de certains indicateurs
-
anticiper des phénomènes — certains diront “prédire d’avenir”… — en détectant des tendances dans des ensembles de données ou dataset provenant d’une ou plusieurs sources (phénomène de corrélation).
-
créer de nouveaux contenus en réponse à des requêtes (→ IAs génératives).
Elle est donc utilisée dans de nombreux domaines :
-
L’intelligence artificelle générative (→ Machine Learning et Deep Learning)
-
La robotique
-
La reconnaissance automatique (vocale, faciale, de forme…)
-
L’internet des objets (→ IoT pour Internet of Things)
-
Les processus industriels (→ Industrie 4.0)
-
L’économie
-
Les prévisions météo
-
…
Étapes d’un projet de science de données
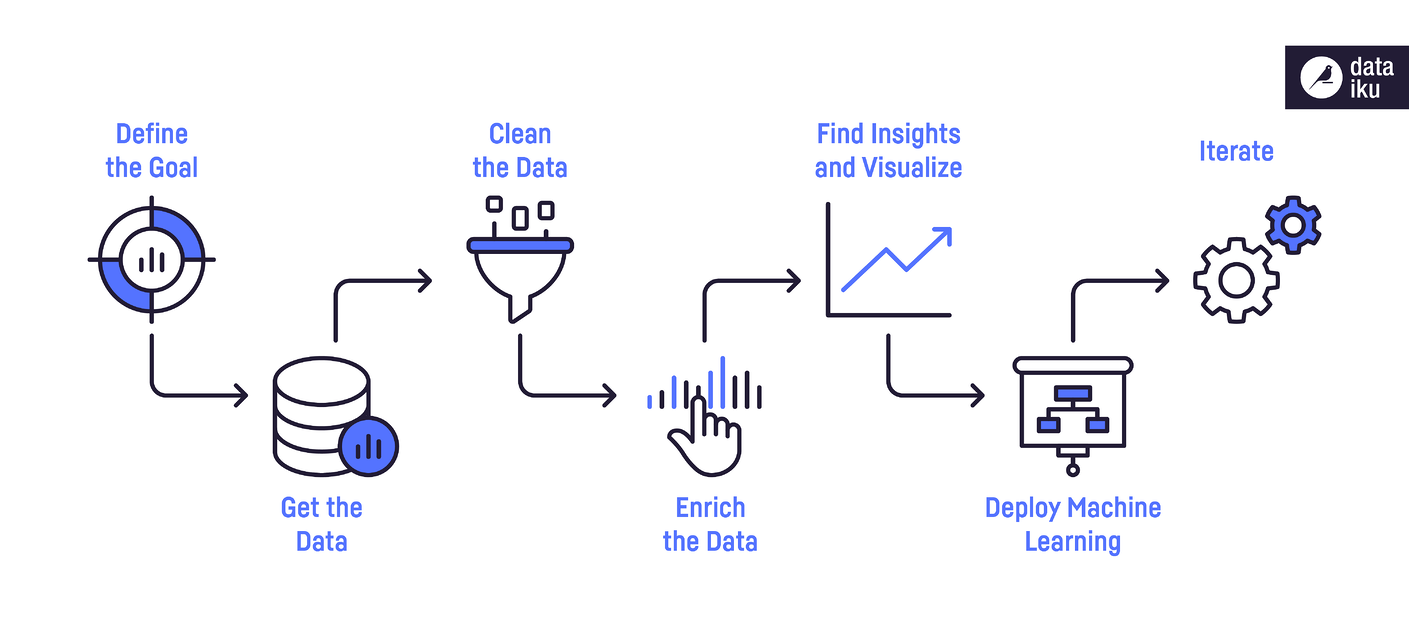
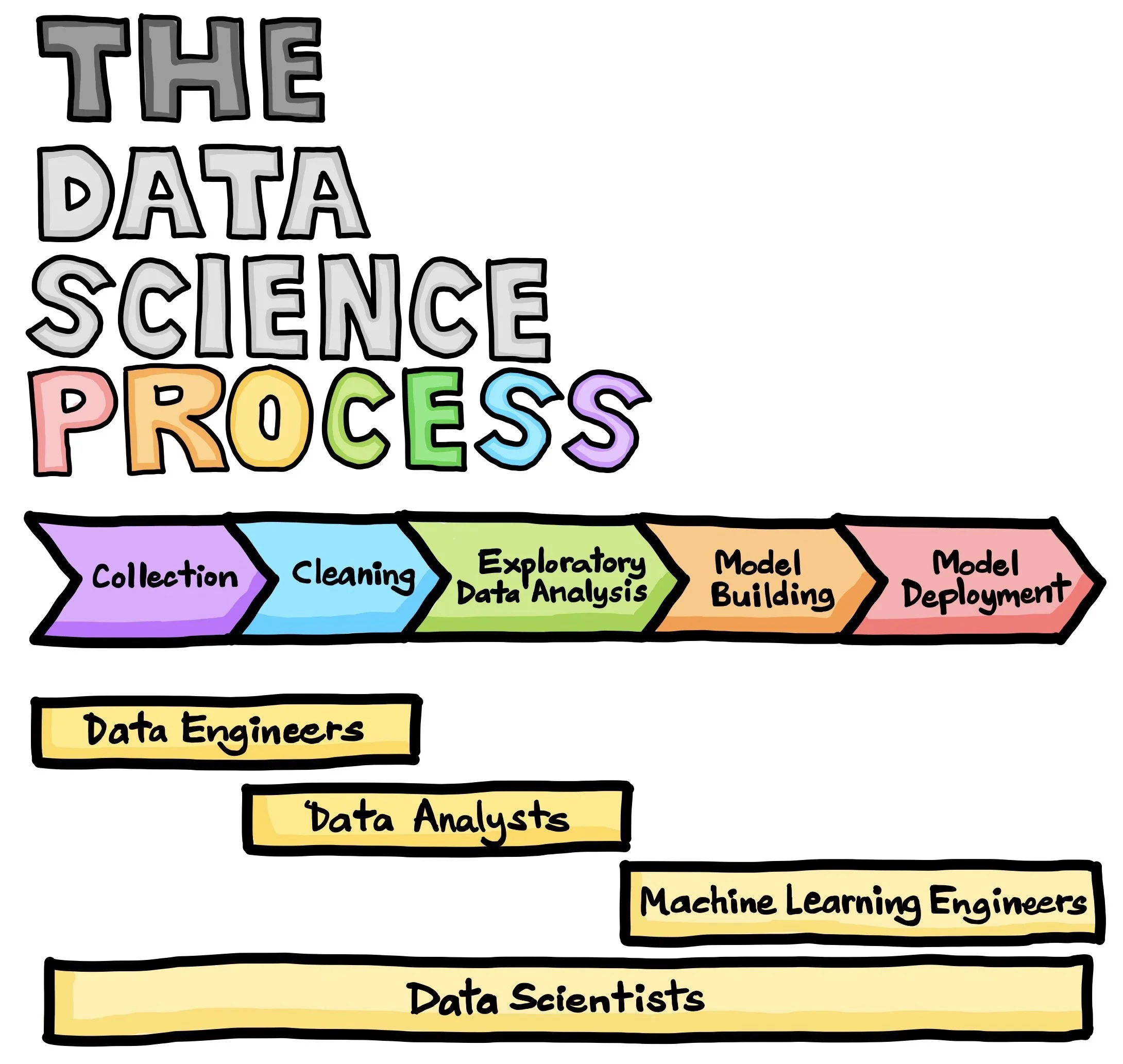
Quel que soit le domaine d’utilisation, on peut concevoir que plusieurs étapes préparatoires sont nécessaires avant l’exploitation des données dans un modèle :
-
Définir l’objectif
-
Récolter les données
-
Nettoyer les données
-
Enrichir les données
-
Sélectionner les informations pertinentes et les visualiser
(voir 7 Fundamental Steps to Complete a Data Analytics Project pour plus de détails sur ces étapes).
On retrouve typiquement ces 5 étapes dans un projet de Machine Learning :
Visualisation des données
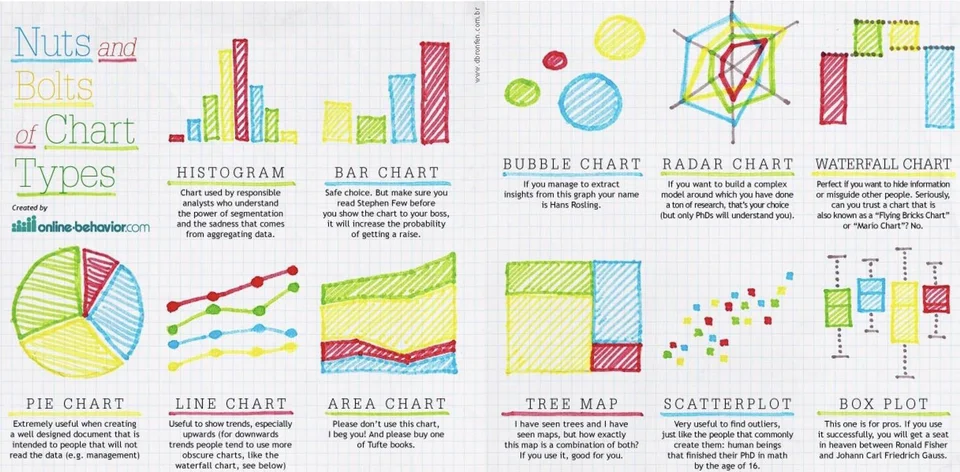
Dans un projet de science des données, la visualisation de ces dernières sous forme de graphiques est particulièrement importante.
Ces graphiques peuvent mettre en évidence des relations difficilement détectables par l’analyse directe des données , de par leur multitude.
De nombreux graphiques existent pour représenter les données et Python est capable de tracer la majorité d’entre eux.
Le choix d’un graphique en particulier sera dicté par ce que l’analyste veut montrer, comprendre ou expliquer sur les données qu’il étudie.
Numpy
Présentation générale
Numpy est une bibliothèque Python qui met à disposition un grand nombre de fonctions performantes qui permettent essentiellement de manipuler des tableaux de nombres.
Elle est donc largement utilisée dans le domaine de la science des données.
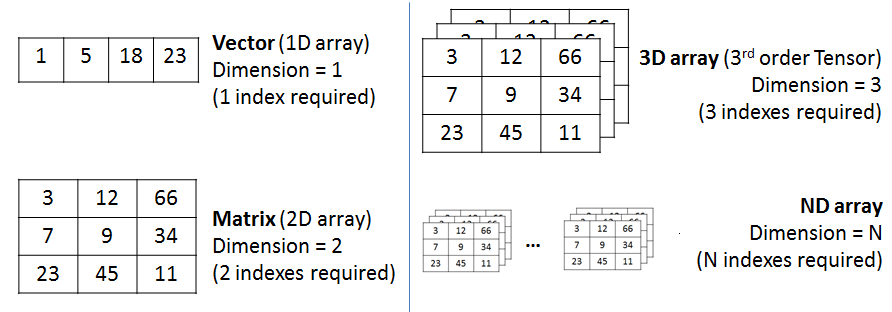
Au cœur de cette librairie on trouve un nouveau type de donnée nommé ndarray (pour N dimensions array ou tableau à N dimensions en français).
Le ndarray correspond globalement à une liste Python — à une ou plusieurs dimensions — mais en beaucoup plus performant en terme de vitesse et d’occupation mémoire.
Outre la performance, on aura également accès à beaucoup plus de fonctions utiles dans le calcul scientifique que celles proposées pour les listes Python.
Cependant, contrairement à une liste Python un ndarray :
-
ne peut contenir que des valeurs de même type (c.-à-d. que des entiers, que des flottants, que des chaînes de caractères…).
-
nécessite d’importer une librairie (→
import numpy as np) pour être pris en charge par Python
Domaines d’utilisation
Comme mentionné plus haut, Numpy est utilisable dans beaucoup de domaines de la science des données :
-
le calcul scientifique.
Exemple : le calcul matriciel
Pour faire le calcul suivant (multiplication de matrices) :
Il suffira de taper le code suivant :
import numpy as np A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[10, 11],[20, 21],[30, 31]]) M = np.dot(A, B) print(M) # Affiche : # [[140 146] # [320 335]]
-
l’analyse et le traitement des données
-
le machine learning et l’intelligence artificielle
-
le traitement d’images et de signaux
Exemple : Zoom sur une image
from scipy import misc import matplotlib.pyplot as plt face = misc.face(gray=True) (1) plt.figure() plt.subplot(2,1, 1) plt.imshow(face,cmap=plt.cm.gray) (2) plt.subplot(2, 1, 2) h = face.shape[0] # hauteur de l'image w = face.shape[1] # largeur de l'image zoom_face = face[h//4 : -h//4, w//4 : -w//4] (3) plt.imshow(zoom_face,cmap=plt.cm.gray) (4) plt.show()1 On stocke dans le ndarray nommé facel’image de référence fournie dans le modulemiscde la librairiescipy(basée surnumpy) et qui fait 1024x768 points2 On affiche l’image complète 3 On crée un nouveau ndarray zoom_facequi contient uniquement les 512x384 points de la partie centrale de l’image originale (→ zoom x2) en utilisant la technique du slicing4 On affiche l’image correspondant à zoom_face
-
La finance et l’économie
-
L’astronomie, la météorologie, la climatologie
-
Le développement de jeux (simulations physiques. Ex. : déplacements, trajectoires…)
-
…
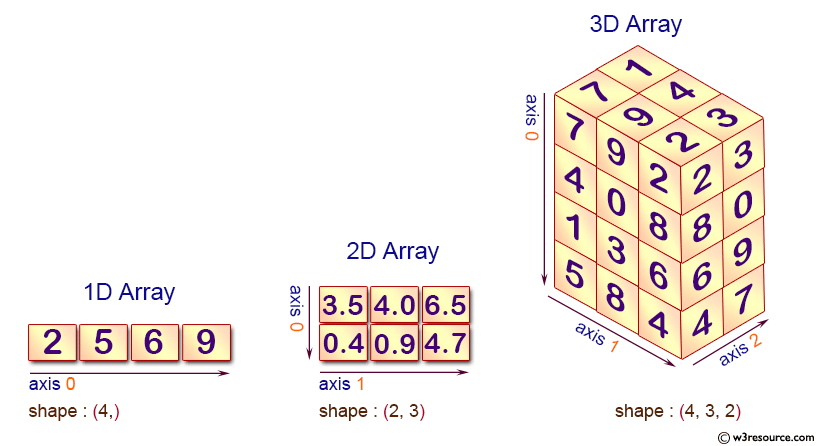
Géométrie d’un ndarray
Lorsqu’on utilise un ndarray, il est essentiel de savoir quelle est sa “géométrie” pour savoir comment accéder à ses éléments.
Cette information nous est retournée par l’attribut shape d’un ndarray.
Celui-ci est un tuple dont les constituants indique le nombre de cases du `ndarray`_ selon les différents axes de celui-ci.
Dans un ndarray à 2 dimensions, l’axe 0 est celui des lignes et l’axe 1, celui des colonnes comme l’illustre la figure suivante (qui fait également apparaître un ndarray à 1 puis à 3 dimensions).
Lorsqu’on voudra accéder aux éléments d’un ndarray (1 ligne, 1 colonne, 1 case, 1 ensemble de cases attenantes dans plusieurs lignes et colonnes …), ce n° d’axe indiquera le rang de l’indice à spécifier pour extraire les données désirées.
ndarray à 2 dimensions :ndarrayNumpy = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]])
print(f'. le tableau : \n{ndarrayNumpy}')
print(f'. sa géométrie : {ndarrayNumpy.shape}')
thirdLine = ndarrayNumpy[2]
print(f'. sa 3ème ligne : {thirdLine}')
print(f'. le 2ème élément de sa 4ème ligne : {ndarrayNumpy[3, 1]}')
print(f'. les 2 derniers éléments des 2 dernières lignes :\n {ndarrayNumpy[-2:, -2:]}')
"""
Affiche :
. le tableau :
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
. sa géométrie : (4, 3)
. sa 3ème ligne : [7 8 9]
. le 2ème élément de sa 4ème ligne : 11
. les 2 derniers éléments des 2 dernières lignes :
[[ 8 9]
[11 12]]
"""Initialisation d’un ndarray
En dehors de l’initialisation avec la méthode array() vue dans les exemples précédents, Numpy propose d’autres fonctions pour créer des ndarrays soit depuis des données existantes, soit en les générant lui-même.
Exemples :
-
np.arange(10)→ crée un tableau d'1 ligne de 10 cases contenant la séquence de nombres [0…9]
(équivalent à la fonctionrange()mais pour desndarrays)>>> np.arange(10) array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) -
np.linspace(0, 1, 5)→ permet d’obtenir un tableau d'1 ligne dont les cases contiennent une séquence de nombres allant d’une valeur de départ (0) à une valeur de fin (1) avec un nombre donné d’éléments (5)>>> np.linspace(0, 1, 5) array([0. , 0.25, 0.5 , 0.75, 1. ]) -
np.empty( (3,2) )→ crée un tableau non initialisé de 3 lignes et 2 colonnes (non initialisé signifie que le contenu des cases est arbitraire)(comath) C:\Users\claud>python >>> np.empty( (3,2) ) array([[7.485e-321, 7.485e-321], [7.485e-321, 7.485e-321], [7.485e-321, 7.485e-321]]) (1) >>> exit() (comath) C:\Users\claud>python >>> np.empty( (3,2) ) array([[1.11261095e-306, 1.37961302e-306], [1.05699242e-307, 1.60218763e-306], [1.69121367e-306, 6.23040373e-307]]) (1) >>>1 Entre 2 instances de Python, on voit bien que le contenu des cases est différent -
np.zeros( (2,5) )→ crée un tableau de 2 lignes et 5 colonnes dont les cases sont initialisées à 0>>> np.zeros( (2,5) ) array([[0., 0., 0., 0., 0.], [0., 0., 0., 0., 0.]]) -
np.full((1, 3), 3.14)→ crée un tableau de 1 ligne et 3 colonnes dont chaque case est initialisée avec la valeur 3.14>>> np.full((1, 3), 3.14) array([[3.14, 3.14, 3.14]]) -
np.genfromtxt('fichier.csv',delimiter=',',skip_header=1)→ initialise un tableau avec le contenu d’un fichier csv (→ coma separated values) en omettant sa 1ère ligne
Accès aux éléments d’un ndarray
L’accès aux éléments d’un ndarray peut se faire de multiples façons :
-
l'indexing
-
le slicing
-
le boolean indexing
L'indexing
C’est la façon la plus intuitive pour accéder à la valeur contenue dans une case d’un nd_array.
Elle utilise simplement les indices de cette case sur les différents axes.
Exemple : Soit le ndarray à 3 dimensions suivant :
On désire accéder aux valeurs 44, 74 et 25.
Le code Python correspondant est :
>>> import numpy as np
>>> values = np.array([[[12, 25, 33]
... , [74, 11, 64]
... , [88, 29, 77]]
...
... , [[44, 58, 42]
... , [-1, -1, 18]
... , [-1, -1, 97]]
...
... , [[68, 81, 22]
... , [-1, -1, 37]
... , [-1, -1, 21]]])
>>> values[1, 0, 0] # 2ème case axe 0
44
>>> values[0, 1, 0] # 2ème case axe 1
74
>>> values[0, 0, 1] # 2ème case axe 2
25|
Voir la vidéo suivante pour une explication de l’indexing sur un ndarray à 2 dimensions. |
Le slicing
Le slicing — comme son nom l’indique (slice signifie “tranche”) — va permettre de découper un ndarray de façon à en récupérer qu’une partie.
Ceci sera obtenu en spécifiant entre crochets un index de début et un index de fin (séparés par ‘:’) sur chacun des axes du ndarray que l’on souhaite découper.
Exemple : Dans le ndarray représenté ci-dessous, les valeurs des cases bleues seront extraites avec l’instruction values[0:1, 1:3, 0:4]
>>> values[0:1, 1:3, 0:3]
array([[[74, 11, 64],
[88, 29, 77]]])|
Noter que la case spécifiée par l’indice de fin n’est pas incluse dans le résultat du slicing (on s’arrête à la case d’avant) |
Lorsqu’on omet l’indice de départ, la zone découpée commence au 1er élement de l’axe du ndarray.
De même, si on omet l’indice de fin, la zone découpée finit au dernier élément de l’axe du ndarray
En conséquence, si on omet les 2, et donc qu’on spécifie seulement ‘:’, c’est l’ensemble des cellule de l’axe considéré qui est retourné.
Exemple : Extraction des portions colorées dans le ndarray suivant
>>> values[:2,0:1,0:1] # axe 0, 1ère case -> 2ème case
array([[[12]],
[[44]]])
>>> values[1:2,1:,2:3] # axe 1, 2ème case -> dernière case
array([[[18],
[97]]])
>>> values[0:1,:,1:2] # axe 1, toutes les cases
array([[[25],
[11],
[29]]])|
On ne le traitera pas ici mais d’autres syntaxes sont encore possibles (indice négatif, spécification de saut). Voir l’article Python Slice Notation: Quick Explanation |
Le boolean indexing
La dernière façon d’accéder à des des portions de ndarray consiste à cibler uniquement les cases qui répondent à certaines conditions.
Ceci se fera en spécifiant une expression booléenne à l’intérieur de la paire de crochets plutôt que des indices.
|
Lorsqu’on extrait des cases d’un ndarray avec le boolean indexing, la géométrie (→ shape) du tableau retourné n’est pas conservée. Exemple : sélectionner les cases dont la valeur est supérieure à 50 dans le ndarray suivant : Par contre, l’accès en écriture dans un ndarray à l’aide du boolean indexing ne modifie pas la géométrie du ndarray d’origine Exemple : Remplacer par 0 toutes les valeurs de ce même ndarray supérieures à 50 |
Matplotlib
Présentation générale
Matplotlib est la bibliothèque Python de tracé de graphique la plus populaire.
Cette librairie couvre de nombreux types de graphes : lignes, courbes, histogrammes, points, barres, camembert, tableaux, polaires, …
Un aperçu des courbes qu’elle peut tracer est consultable sur Matplotlib > Gallery
De manière générale, à chaque type de graphique est associé une fonction (ex : hist() pour un histogramme) à laquelle il va falloir fournir — pour une courbe à 2 dimensions — les points correspondant aux abscisses puis ceux correspondant aux ordonnées.
Ces points peuvent être fournis sous forme de tuples ou listes Python mais, en règle générale, on les passera souvent sous forme de ndarrays ou de series ou bien encore de dataframes qui sont des types d’ensemble de données définis dans les librairies Numpy et Pandas.
|
Même si sa mise en œuvre est simple pour un usage basique, la structure de Matplotlib et son fonctionnement interne font que son utilisation peut être déroutante dans le cadre de tracés plus complexes si on ne maîtrise pas ses concepts de base. |
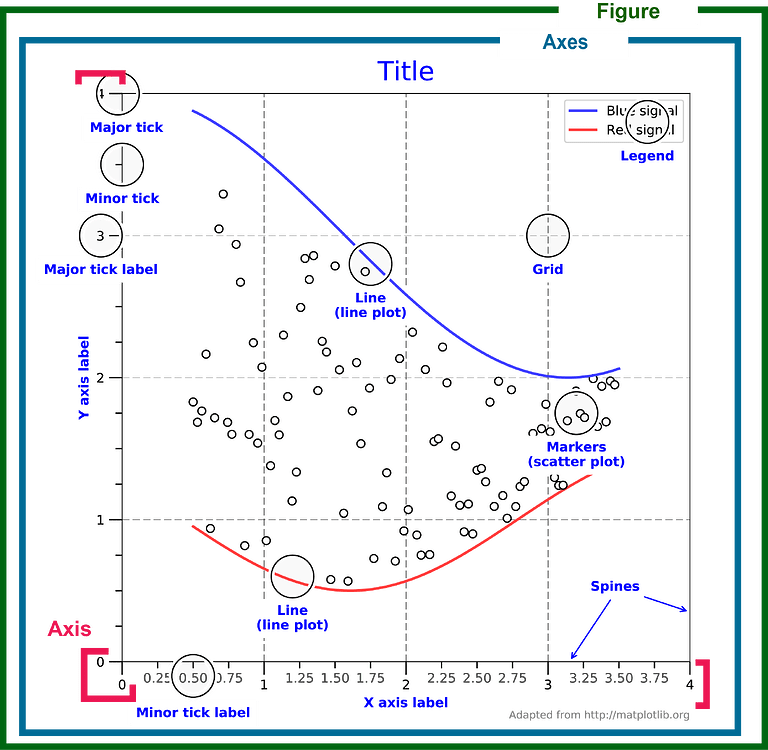
Anatomie d’une figure Matplotlib
Une figure Matplotlib peut contenir 1 ou plusieurs “zones de tracé” qui sont appelées “axes” dans la documentation.
|
Le terme axe peut prêter à confusion en français puisque dans Matplotlib ceci correspond à une “sous-figure” alors que pour nous, les axes représentent plutôt les droites graduées d’un système de coordonnées cartésiennes (→ axe des abscisses, axe des ordonnées). Ces dernières sont appelées axis dans Matplotlib. |
Un “axe” Matplotlib encapsule plusieurs éléments importants :
-
Les données tracées (lignes, points, barres, etc.)
-
Les axes X et Y avec leurs graduations et étiquettes
-
Un titre
-
Une légende (optionnelle)
-
Des grilles (optionnelles)
Utilisation basique
Admettons que l’on veuille tracer la fonction suivante sous forme de courbe :
Le code Python sera alors :
import numpy as np
# Importation du module de tracé de Matplotlib
import matplotlib.pyplot as plt
# Importation du module de gestion des graduations de Matplotlib
import matplotlib.ticker as tck (2)
# Définition de la fonction f(x)
# !! IMPORTANT !! Cette fonction acceptera un ndarray en
# paramètre et sera capable d'appliquer l'exposant à chacun
# de ses éléments sans devoir faire de boucle car l'opérateur
# `**` est considéré comme une "ufunc" dans Numpy (1)
def f(x) : (3)
y = x ** 2
return y
# Domaine de définition de la fonction : [0...10[
# => Définition d'un ndarray contenant 100 valeurs de 0 à 9
# également réparties
x = np.linspace(0,9,100) (4)
# Appel de la fonction pour calculer le carré de toutes les
# valeurs contenues dans `x`
y = f(x) (5)
# Création d'une figure Matplotlib
fig, ax = plt.subplots(layout="constrained")
# Configuration de la grille de la courbe :
# . une graduation horizontale principale toutes les 1 unités
ax.xaxis.set_major_locator(tck.MultipleLocator(1))
# . une graduation horizontale secondaire toutes les 0.5 unités
ax.xaxis.set_minor_locator(tck.MultipleLocator(0.5))
# . une graduation verticale principale toutes les 10 unités
ax.yaxis.set_major_locator(tck.MultipleLocator(10))
# . une graduation verticale secondaire toutes les 0.5 unités
ax.yaxis.set_minor_locator(tck.MultipleLocator(5))
# . styles des grilles principales et secondaires
ax.grid(which='major', color='#CCCCCC', linestyle='--')
ax.grid(which='minor', color='#CCCCCC', linestyle=':')
# Tracé de la fonction
ax.plot(x, y, "blue")
# Configuration de la figure :
# . libellé axe des abscisses
ax.set_xlabel("abscisses")
# . libellé axe des ordonnées
ax.set_ylabel("ordonnées")
# . titre de la figure
ax.set_title("Fonction carré")
# . légende de la figure placée en haut à gauche
# et définie sous forme de code LATEX
ax.legend([r'$ f(x) = x^{2}$' ], loc='upper left')
# Affichage de la figure
plt.show()| 1 | Voir ufunc ( Universal function) |
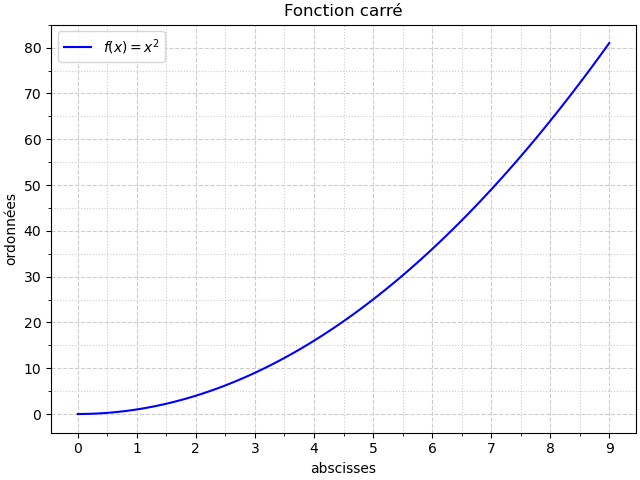
On obtient alors :
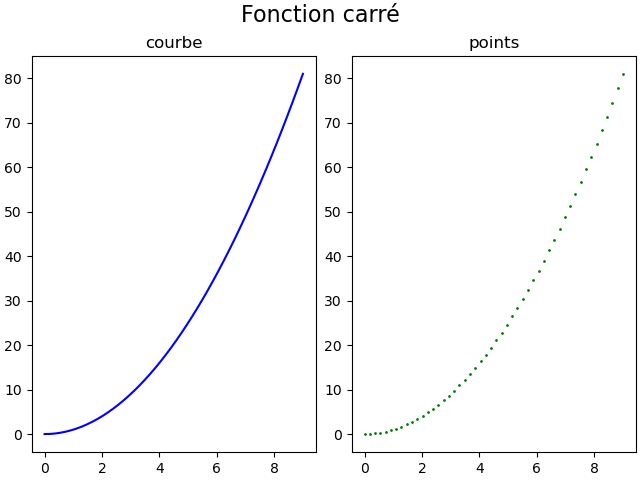
Si on veut afficher plusieurs graphiques sur une même figure, on peut utiliser la fonction subplots(<nb-lignes>, <nb-colonnes>, …)
Pour tracer notre fonction sous forme de courbe et de points dans 2 graphiques côte-à-côte, le code Python devient alors :
import numpy as np
import matplotlib.pyplot as plt
def f(x) :
y = x ** 2
return y
# Domaine de définition de la fonction : [0...10[
# Définition d'un ndarray contenant 50 valeurs de 0 à 9 également réparties
x = np.linspace(0,9,50)
# Calcul des images de la fonction
y = f(x)
# Création d'une figure Matplotlib comportant 2 sous-figures
fig, (ax1, ax2) = plt.subplots(1,2,layout="constrained")
# Tracé de la fonction sous forme de courbe puis sous forme de points
ax1.plot(x, y, "blue")
ax2.scatter(x, y, 1.0, "green")
# Configuration de la figure
fig.suptitle('Fonction carré', fontsize=16)
ax1.set_title("courbe")
ax2.set_title("points")
# Affichage de la figure
plt.show()🞄 🞄 🞄