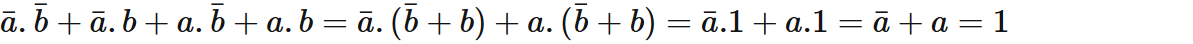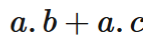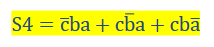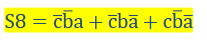1. Introduction
1.1. La variable logique.
Pour illustrer le concept de variable logique, imaginons que vous disposiez d’un capteur de température et d’un capteur d’hygrométrie. Ces deux capteurs sont indépendants et fournissent des valeurs de deux grandeurs physiques différentes et indépendantes.
En général, de tels capteurs fournissent des valeurs analogiques. Imaginons, à présent, que vous définissiez une variable a de la façon suivante : si la température est supérieure à une valeur de seuil, 15° C, par exemple, cette variable est à 1 (ou Vrai, ou Haut). Dans le contraire, si la température est inférieure à ce seuil, la variable est à 0 (ou Faux, ou Bas).
De façon analogue, vous définissez la variable b relativement à l’hygrométrie comparée à une valeur seuil.
|
Chacune de ces deux variables ne peut prendre que deux valeurs distinctes. On peut noter ces deux valeurs 0 et 1, mais il faut comprendre alors que dans ce contexte, 0 et 1 n’ont pas valeur de nombre. Ce sont de simples étiquettes qui décrivent l’état logique de la variable. |
2. Les fonctions logiques élémentaires.
Les fonctions ou portes élémentaires qui suivent, définissent des fonctions qui élaborent une sortie en fonction des entrées de ces variables logiques.
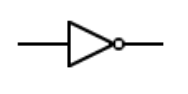
2.1. La porte NON.
La porte NON, appelée aussi porte inverseuse ou simplement inverseur, possède une entrée unique, notée ici a.
La sortie est notée:
sa fonction est conforme à la table de vérité ci-dessous :
| a | s |
|---|---|
0 |
1 |
1 |
0 |
On dit aussi que la sortie est complémentée. La porte NON est la fonction de complémentation.
Cette porte, pour très simple et basique qu’elle soit, est cruciale puisque nous verrons plus loin que dans les expressions algébriques qui décrivent toute fonction combinatoire, cette fonction ou opération de complémentation est omniprésente.
La représentation symbolique graphique de cette porte existe selon deux normes qu’il faut connaître :
| La norme internationale et européenne en vigueur : | La norme américaine |
|---|---|
norme internationale, IEEE |
théoriquement désuète, mais encore beaucoup utilisée par les praticiens : |
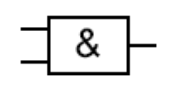
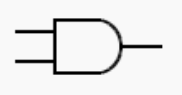
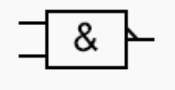
2.2. Porte ET/AND à deux entrées.
La porte ET ou AND à deux entrées, notées ici a et b , peut être décrite comme suit : La sortie est notée:
la sortie est à 1 lorsque les deux entrées sont à 1.
Cette fonction, ou porte, est ainsi définie en langue naturelle. Il est donc aisé d’écrire sa table de vérité :
| a | b | s=a.b |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
Il faut bien comprendre que dans la notation s=a.b, le point représente la fonction logique ET, non la multiplication arithmétique usuelle. Toutefois, lorsqu’on effectue le produit arithmétique usuel sur les variables logiques décrites en 0 et 1, on obtient le même résultat. Il y a un lien avec le produit arithmétique usuel, mais il ne faut toutefois pas faire la confusion. |
| La norme internationale et européenne en vigueur : | La norme américaine |
|---|---|
norme internationale, IEEE |
théoriquement désuète, mais encore beaucoup utilisée par les praticiens : |
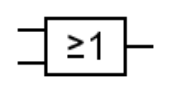
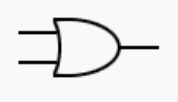
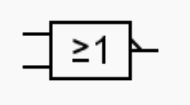
2.3. Porte OU/OR à deux entrées.
Avec les mêmes notations, la sortie est notée:
La sortie est à 1 si une entrée au moins est à 1.
Là encore, la définition de cette porte élémentaire est donnée en langue naturelle.
La table de vérité est immédiate selon :
| a | b | s=a+b |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
Là aussi, la notation +, dans ce contexte, désigne la fonction logique OU et non l’addition arithmétique usuelle. D’ailleurs, si on fait l’addition arithmétique usuelle sur les entrées en 0 et 1, on ne trouve évidemment pas un résultat correct : 1+1=2 en arithmétique usuelle, tandis que 1+1=1 dans le contexte de la logique binaire. |
| La norme internationale et européenne en vigueur : | La norme américaine |
|---|---|
norme internationale, IEEE |
théoriquement désuète, mais encore beaucoup utilisée par les praticiens : |
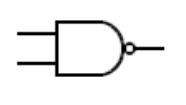
2.4. Porte NAND à deux entrées.
En combinant la porte ET*et la porte *NON, on définit une nouvelle fonction logique élémentaire, la porte NON-ET plutôt désignée par son équivalent anglais, la porte NAND. On l’obtient par l’équation:
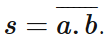
Pour obtenir sa table de vérité, on commence par faire le ET logique entre les deux entrées, puis on complémente le tout. On obtient :
| a | b | a.b | s |
|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
| La norme internationale et européenne en vigueur : | La norme américaine |
|---|---|
norme internationale, IEEE |
|
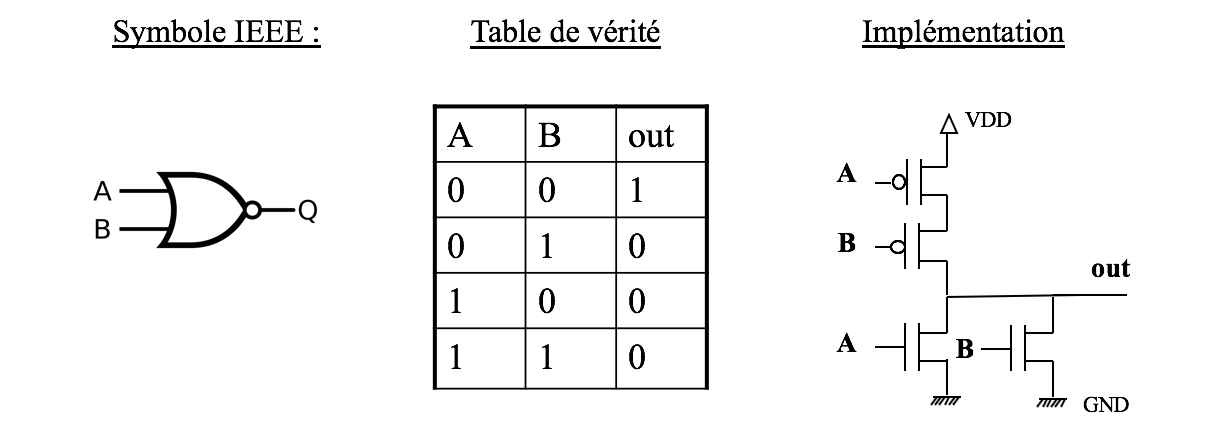
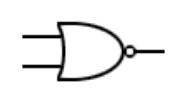
2.5. Porte NOR à deux entrées.
De façon analogue, on peut introduire la porte NON-OU ou NOR, comme combinaison de la porte OU et de la porte NON. Elle est ainsi définie par l’équation
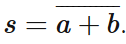
Pour obtenir sa table de vérité, on commence par faire le OU logique entre les deux entrées, puis on complémente le tout. On obtient :
| a | b | a+b | s |
|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
| La norme internationale et européenne en vigueur : | La norme américaine |
|---|---|
norme internationale, IEEE |
|
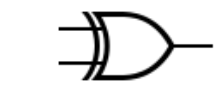
2.6. Porte OU-exclusif ou XOR.
La porte XOR est définie en langue naturelle par la définition suivante : la sortie est à 1 si une entrée et une seule est à 1. On obtient facilement la table de vérité :
Pour obtenir sa table de vérité, on commence par faire le OU logique entre les deux entrées, puis on complémente le tout. On obtient :
| a | b | s |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
Cette nouvelle fonction ou porte peut être écrite sous forme d’expression booléenne comme combinaison des fonctions ET, OU et NON. Toutefois, nous verrons ces éléments dans la prochaine partie. |
| La norme internationale et européenne en vigueur : | La norme américaine |
|---|---|
norme internationale, IEEE |
|
2.7. Exercices:
2.8. Exercices corrigés.
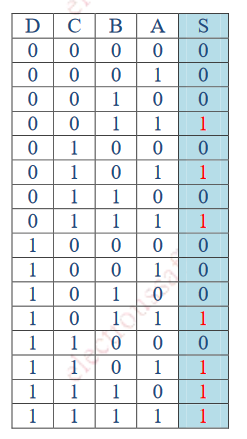
Exercices 1
Donner les équations de S1 et S2
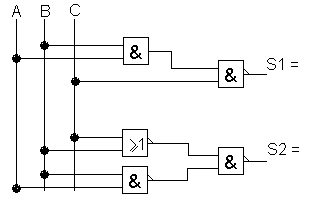
Rechercher sur un brouillon et vous pouvez ensuite vous aider de la correction.
|
Ecrire les équations partielles à chaque sortie. |
Exercices 2
-
Déterminer l’équation du circuit de la figure suivante :
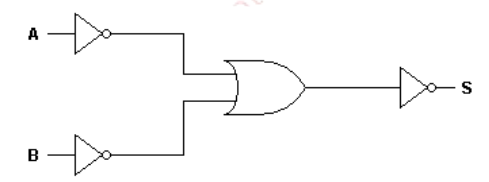
-
Dresser la table de vérité de ce circuit
-
Quelle est la fonction logique réalisée et quel est son symbole?
Exercices 3
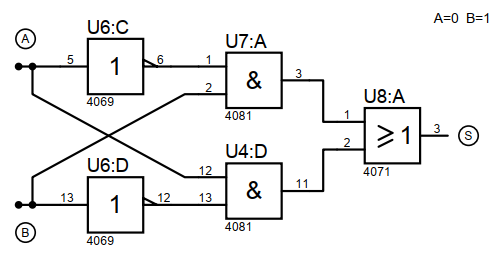
- S = 0
- S = 1
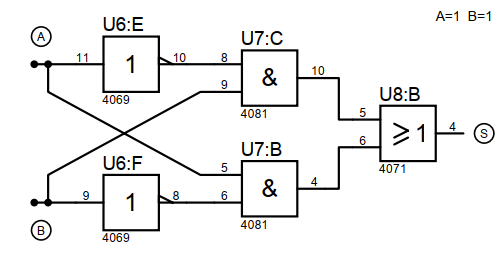
- S = 0
- S = 1
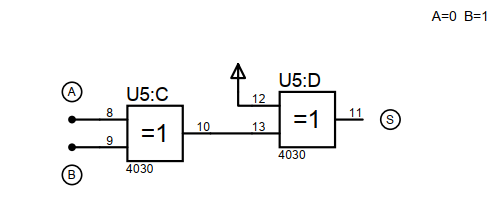
- S = 0
- S = 1
2.9. Exercices:
3. Fonctions avancées.
Nous allons voir maintenant des fonctions avancées construites avec des portes élémentaires. Ces fonctions sont utilisées dans les systèmes numériques.
3.1. Le décodeur.
Ce type de décodeur permet de faire correspondre à un code présent en entrée sur n lignes une sortie et une seule active parmi les N = 2n sorties possibles.
On le désigne aussi par décodeur m lignes vers n lignes.
Pour comprendre le principe d’un tel décodeur, étudions le décodeur 1 parmi 4 ou 2 vers 4:
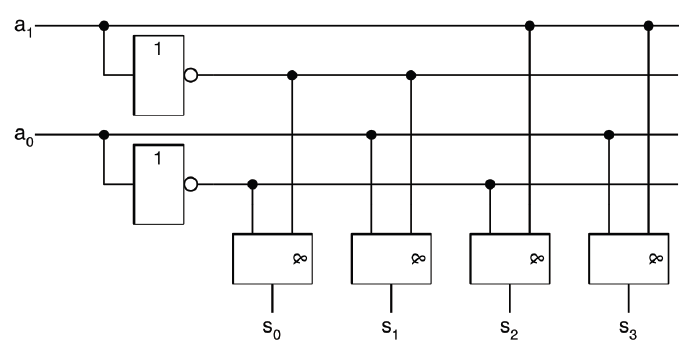
-
Remplir la table de vérité ci-dessous sur votre cahier d’exercice.
a _1 a_0 S_3 S_2 S_1 S_0 0
0
0
1
1
0
1
1
-
Ecrire les équations de chaque sortie.
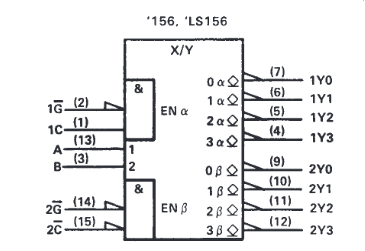
On peut citer comme exemple le double décodeur vendu sous la référence 74LS156 dont le brochage et la table de fonction sont donnés à la figure suivante:
-
Symbole norme IEEE.
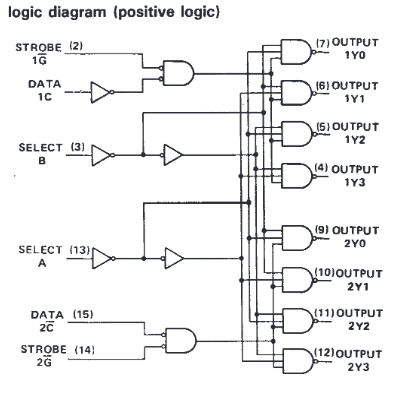
-
Diagramme logique.
-
Table de fonctionnement.
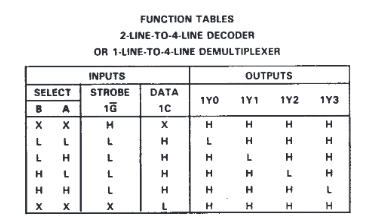
|
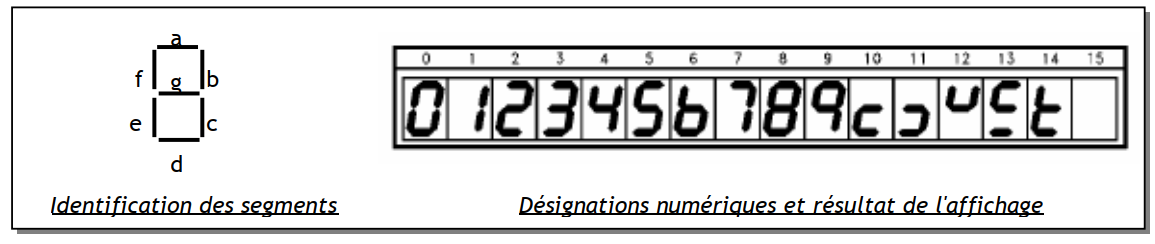
3.1.1. Décodeur BCD – 7 segments.
Ce type de décodeur permet de convertir le code BCD 4bits à l’entrée pour obtenir à la sortie un code 7 segments permettant de commander un afficheur 7 segments permettant l’écriture de tous les chiffres et aussi d’autres symboles comme le montre la figure suivante :
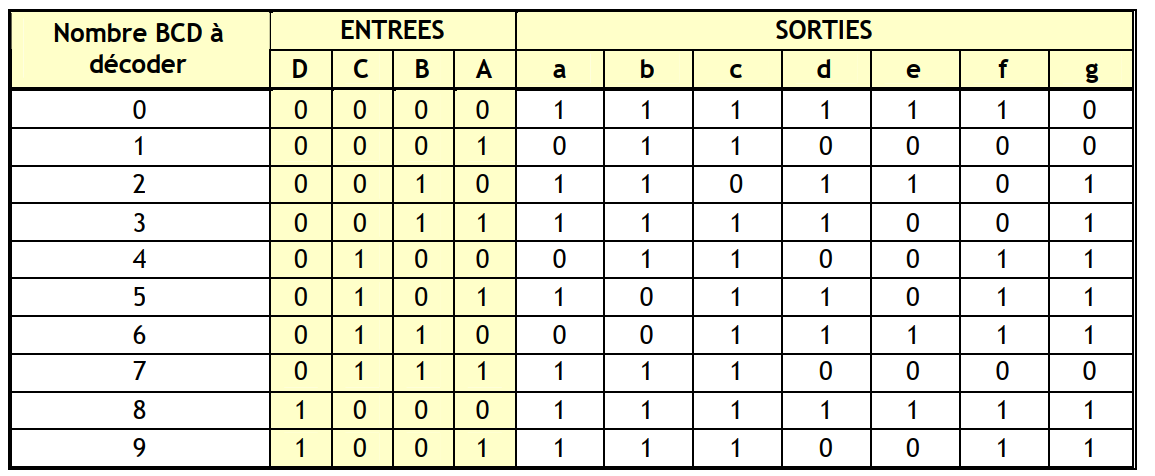
Pour mettre en équation ce type de décodeur, il faut dresser la table de vérité suivante :
3.2. Le multiplexeur.
Un multiplexeur permet de sélectionner une entrée parmi 2n pour transmettre l’information portée par cette ligne à un seul canal de sortie.
La sélection de l’entrée se fait alors à l’aide de n lignes d’adressage (commande).
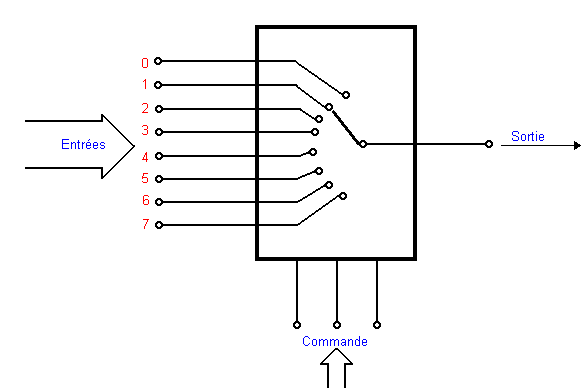
|
La technique de commutation des signaux électroniques numériques est très importante et trouve de nombreuses applications comme la téléphonie mobile. |
Pour comprendre le principe d’un multiplexeur, étudions le multiplexeur 4 voies suivant:
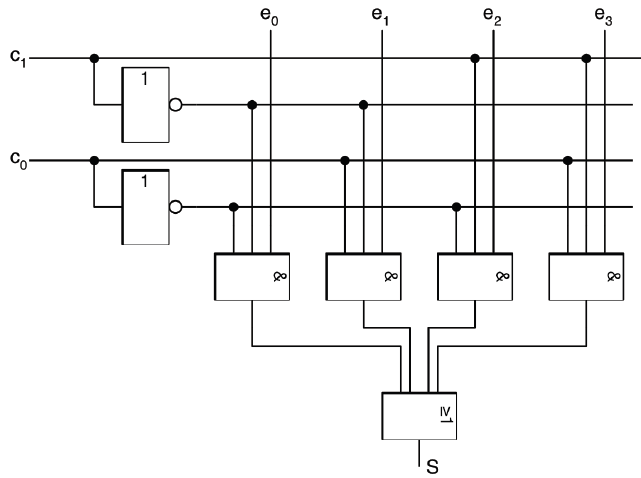
-
Remplir la table de vérité ci-dessous sur votre cahier d’exercice.
c _1 c_0 S 0
0
0
1
1
0
1
1
-
Ecrire les équations de chaque sortie.
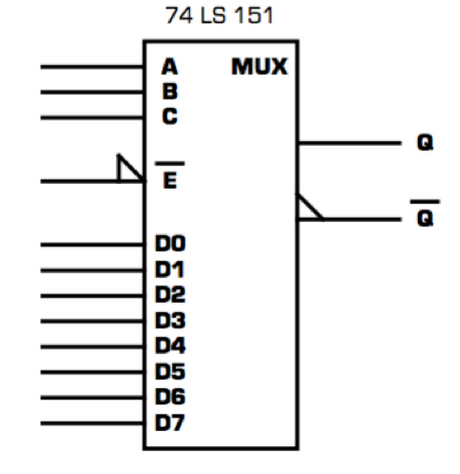
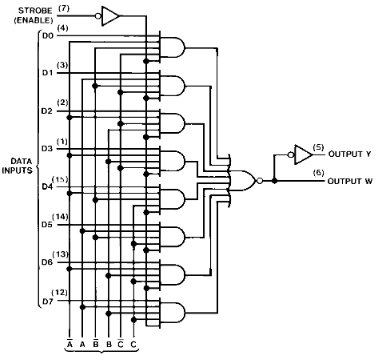
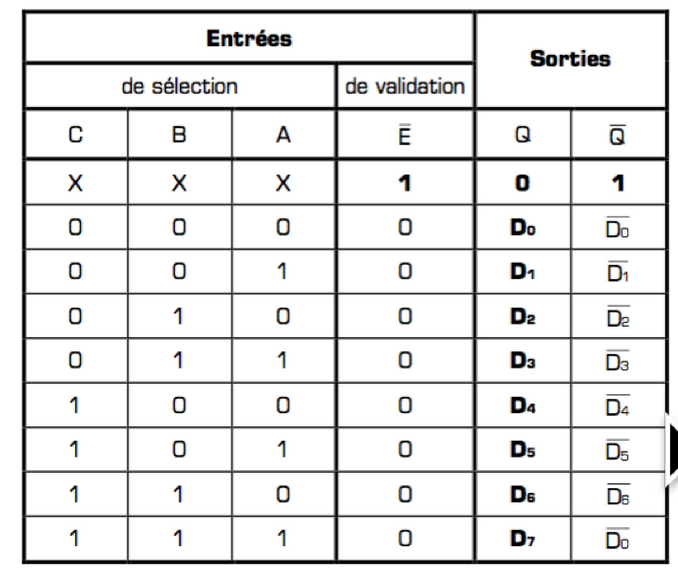
On peut citer comme exemple le multiplexeur 8 vers 1 vendu sous la référence 74LS151:
-
Symbole norme IEEE.
-
Diagramme logique.
-
Table de fonctionnement.
3.2.1. Fiche exercice.
3.3. Autres fonctions.
Il existe de nombreuses autres fonctions réalisées à partir de ces portes élémentaires comme les démultiplexeurs, les comparateurs, additionneurs…
Vous trouverez avec ce lien une liste de quelques fonctions.
Il faut bien comprendre qu’elles sont les briques de base de notre technologie actuelle.
Cependant les avancées de la miniaturisation ont permis d’intégrer toujours plus de ces fonctions sur une même puce. Cela a permis la création de microprocesseurs et de "system on chip", mais cela est une autre histoire que nous vérons dans les prochains parcours de formation.
4. Résolutions de projets simples.
Avec les portes logiques élémentaires nous pouvons résoudre quelques projets élèmentaires.
4.1. Exercices expliqués:
Serrure d’un coffre
Quatre responsables d’une société (A, B, C et D) peuvent avoir accès à un coffre. Ils possèdent chacun une clé différente et il a été convenu que :
-
A ne peut ouvrir le coffre que si au moins un des responsables B ou C est présent.
-
B, C et D ne peuvent l’ouvrir que si au moins deux des autres responsables sont présents.
Donner l’équation logique de la serrure de coffre S.
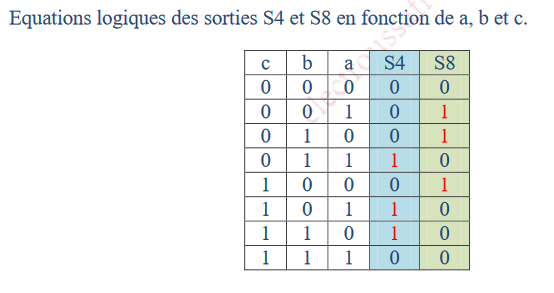
Amplification sonore
Les trois haut-parleurs d’une salle de cinéma (a, b et c) peuvent être branchés sur un amplificateur qui possède deux sorties : la première d’impédance 4 Ω (S4) et la deuxième d’impédance 8 Ω (S8).
-
Lorsqu’un seul haut-parleur est utilisé, il doit être relié à la sortie de 8 Ω.
-
Lorsque deux haut-parleurs sont utilisés, ils doivent être reliés tous les deux à la sortie de 4 Ω (ils sont alors montés en parallèle).
-
Le fonctionnement simultané des trois haut-parleurs est interdit.
Déterminer les équations logiques des sorties S4 et S8 en fonction de a, b et c.
Configuration d’une machine outil
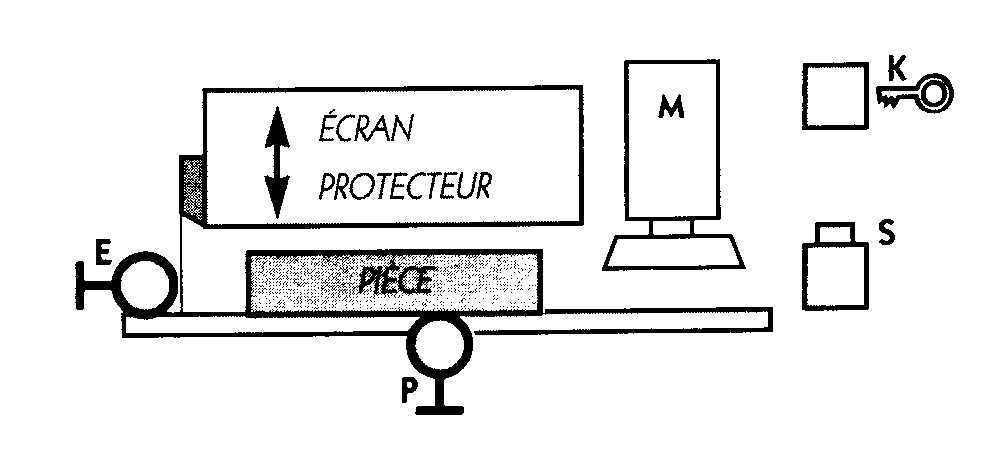
Pour actionner le moteur M de la machine il faut :
En marche normale, la mise en fonctionnement de la machine automatique impose l’ensemble des conditions suivantes :
-
contrôle du bon positionnement de la pièce par P.
-
fermeture de l’écran de protection par E,
-
action sur le capteur S.
En marche réglage cette machine fonctionne :
-
avec ou sans écran de protection
-
La pièce bien positionnée,
-
une clé engagée dans un contact à verrouillage K,
-
action sur le capteur S.
-
Remplir la table de vérité garder la présentation suivante:
-
Donner l’éqution de M.
-
5. Simplification des équations logiques.
Il est important de simplifier ces équations logiques afin de limiter le nombres de portes logiques utilisées (pour des raisons de coût,compléxité, temps d’éxecution…)
L’algébre de boole va nous fournir des outils pour cette simplification.
5.1. Rappel:
les variables n'ont pas de signification numérique mais logique et ne peuvent prendre que deux états dits logiques, notés souvent 0 et 1, même si d'autres notations sont possibles ;
les notations "." et "+" signifient, en algèbre de Boole, les fonctions ET et OU respectivement ;
une fonction logique combinatoire quelconque s'écrit comme combinaison des fonctions logiques ET, OU et NON et peut être écrite comme expression dite booléenne de ces opérateurs.
5.2. Postulats
|
Bien lire 1.1 comme 1 ET 1 , 1 + 1 comme 1 OU 1. |
-
1.1=1, 0+0=0 ;
-
1.0=0.1=0, 0+1=1+0=1 ;
-
0.0=0, 1+1=1 ;
-
1 =0 et 0=1
5.3. Théorèmes
-
Théorème 1 : absorption
0.X=0
1+X=1
-
Théorème 2 : éléments neutres
1.X=X
0+X=X
-
Théorème 3 : idempotence
X+X=X
X.X=X
-
Théorème 5 : associativité
(a+b) + c = a + (b+c) = a+b+c
(a.b).c=a.(b.c)=a.b.c
-
Théorème 6 : commutativité
a+b=b+a
a.b=b.a
-
Théorème 7 : distributivité
a.(b+c)=a.b+a.c
a+(b.c)=(a+b).(a+c)
La première relation nous dit que l'opération ".", c'est-à-dire la fonction ET, est distributive par rapport à la fonction OU. La relation fonctionne aussi pour l'arithmétique usuelle. La deuxième relation nous dit que la fonction OU est distributive par rapport à la fonction ET. Mais la deuxième relation ne fonctionne clairement pas en arithmétique usuelle. Le ET est prioritaire sur le OU , les parenthèses dans le théorème 7 sont indispensables pour la compréhension de l'équation. |
Théorème 8 : simplification
a+a.b=a+b
a.(a+b)=a.b
Théorème 10 : lois de De Morgan
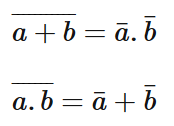
Exercices:
-
En utilisant les théorèmes précédents essayer de démontrer a+a.b=a+b
-
Simplification:
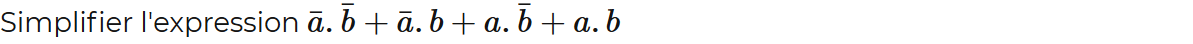
Donner le nom du théorème à chaque étape de calcul.

Donner le nom du théorème à chaque étape de calcul.
-
Simplication des projets précédents.
Vous allez reprendre les projets:
-
Serrure d’un coffre.
-
Amplificateur audio.
-
Machine outil.
Simplifiez les expressions logiques à l’aide de l’algèbre de boole.
-
6. QCM
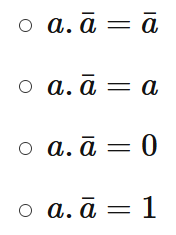
- a
- b
- c
- d
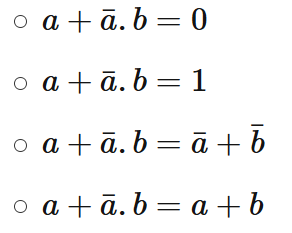
- a
- b
- c
- d
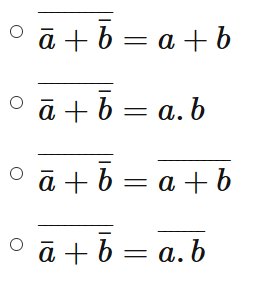
- a
- b
- c
- d
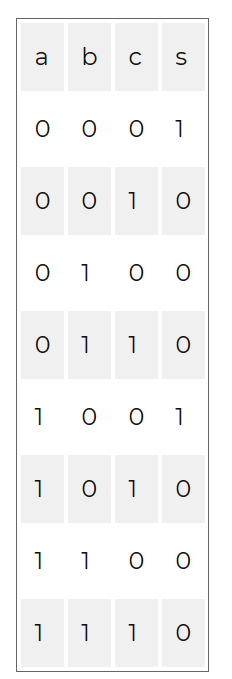
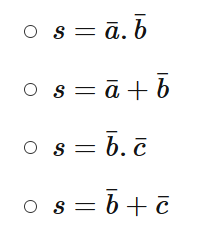
- a
- b
- c
- d
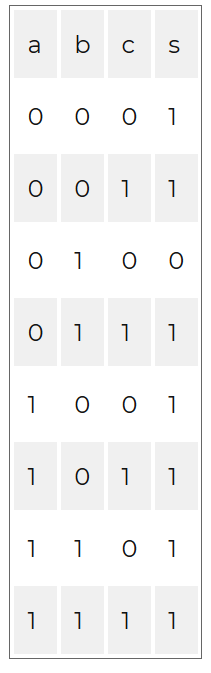
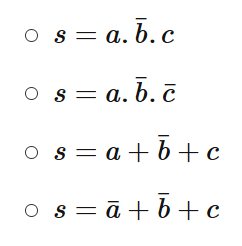
- a
- b
- c
- d
7. Synthèse d’un cahier des charges complet.
8. Aller au bout de la logique…
Nous avons vu que l’intégration de millions de portes logiques élémentaires peut aboutir à un microprocesseur moderne. Mais comment ces portes élèmentaires sont-elles fabriquées et donc les puces électroniques que nous utilisons tous les jours?
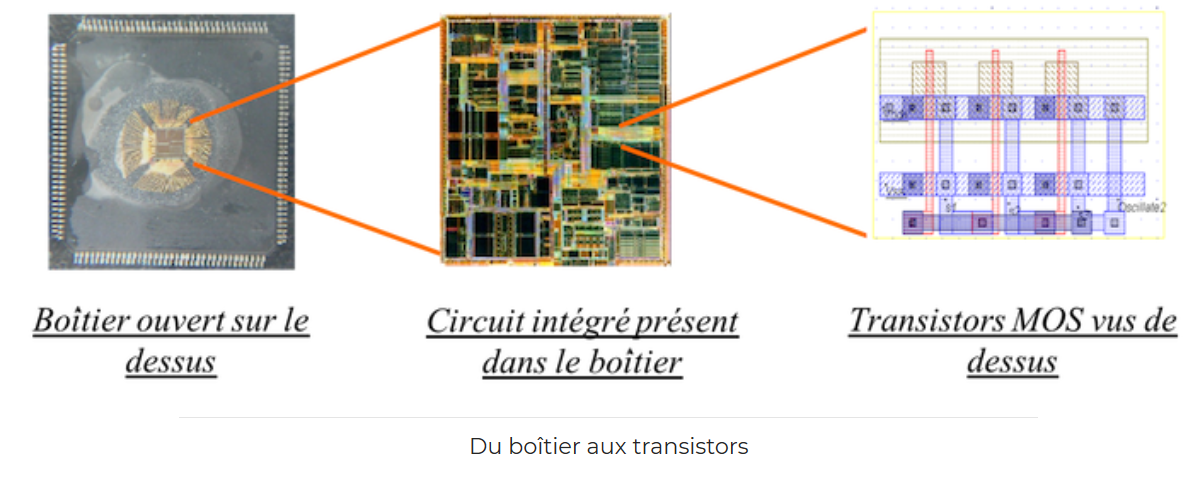
La brique de base du circuit intégré est le transistor.
|
On y trouve aussi des capacités, des résistances, des inductances, des diodes et des interconnexions. |
8.1. Le transistor MOS.
Le transistor MOS est un composant actif ayant 3 broches principales nommées Gate (appelée Grille en français), Drain et Source.
Pour des applications numériques, il fonctionne comme un interrupteur commandé par la Grille et permettant au courant de passer de la Source vers le Drain.
Il est soit en mode ON (le courant circule de la Source vers le Drain) soit en mode OFF (aucun courant ne circule dans le transistor).
Il existe deux types de transistors : le NMOS et le PMOS.
|
Les deux transistors fonctionnent de manière complémentaire :
|
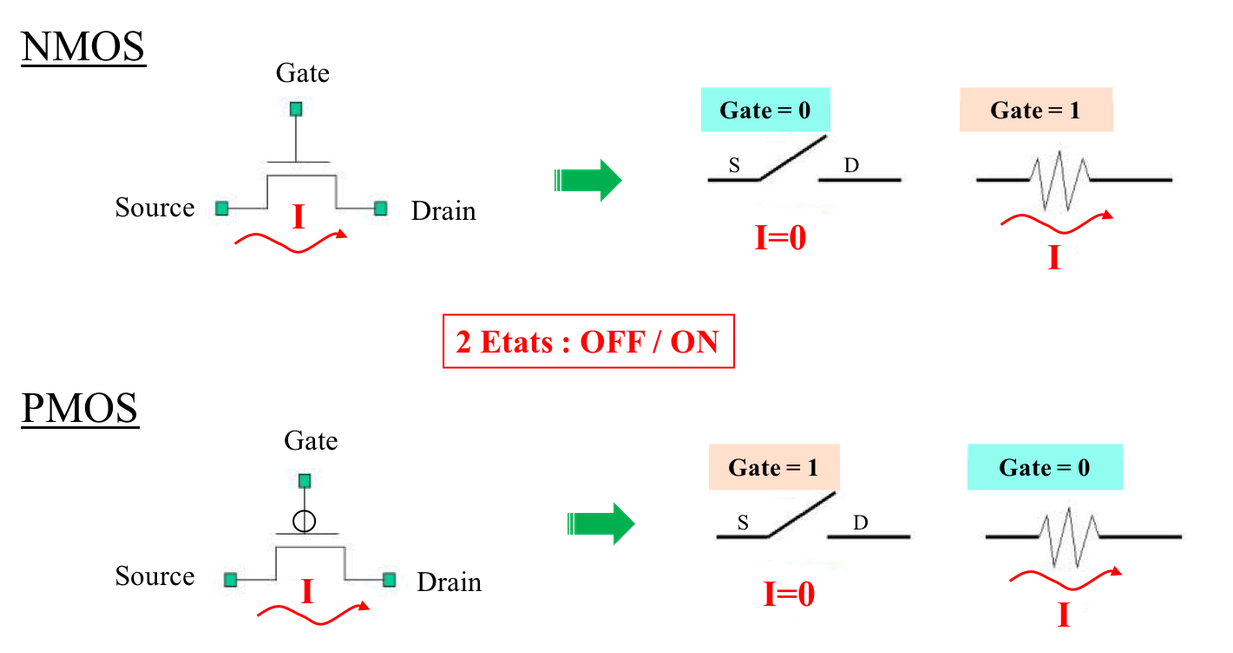
Cette technologie permet de réaliser simplement l’ensemble des fonctions logiques que l’on retrouve à la base des circuits numériques.
8.2. L’inverseur.
L’inverseur est probablement la porte logique la plus simple et la plus utilisée dans la conception de circuits numériques.
L’inverseur CMOS est constitué de deux transistors, un NMOS et un PMOS, connectés en série entre l’alimentation qui constitue le 1 logique et la masse qui représente le 0 logique.
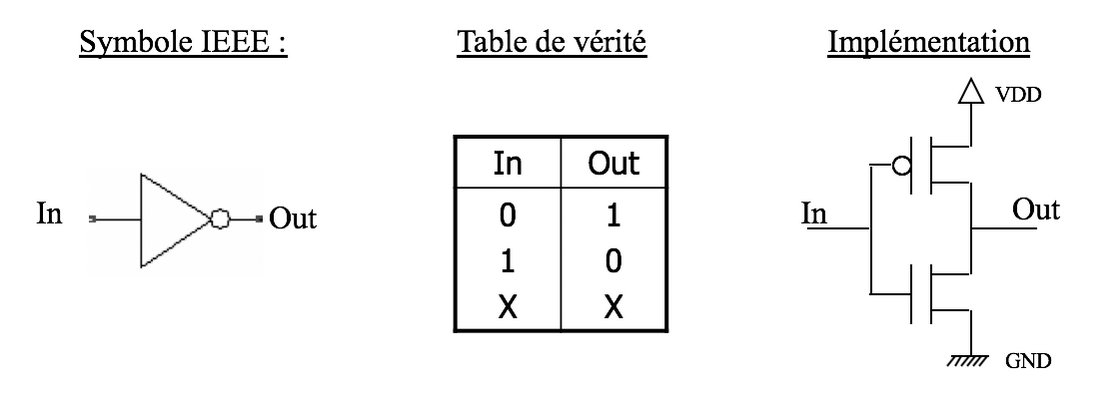
|
La Grille du PMOS et celle du NMOS, reliées, constituent l’entrée de l’inverseur. Le Drain du PMOS et celui du NMOS, reliés, constituent la sortie de l’inverseur. |
|
Gardez en tête que : le transistor NMOS est passant si sa Grille est à 1 ; le transistor PMOS est passant si sa Grille est à 0. |
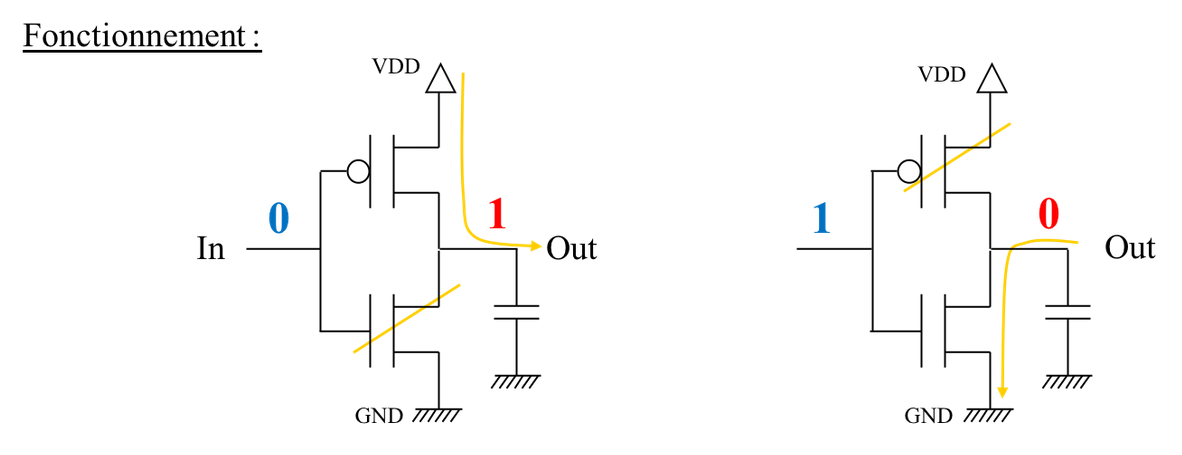
lorsque l'entrée de l'inverseur est au niveau logique Bas (0), seul le transistor PMOS est passant. Un courant circule de l'alimentation VDD vers la sortie OUT et charge la capacité de sortie. La tension de sortie aux bornes de la capacité équivaut alors à un niveau logique haut (1) ;
lorsque l'entrée de l'inverseur est au niveau logique haut (1), seul le transistor NMOS est passant. Le courant se décharge de la capacité de sortie vers la masse et la tension aux bornes de la capacité diminue jusqu’à atteindre le niveau logique bas (0).
En résumé :
un 0 en entrée de l'inverseur donne un 1 en sortie ;
un 1 en entrée de l'inverseur donne un 0 en sortie.
8.3. Autres fonctions.
Toutes les fonctions sont constituées d’un assemblage de transistors MOS. Voici quelques exemples, vous pouvez vous entraîner à déterminer le fonctionnement des transistors en suivant la table de vérité.
-
Porte NAND (NON ET).
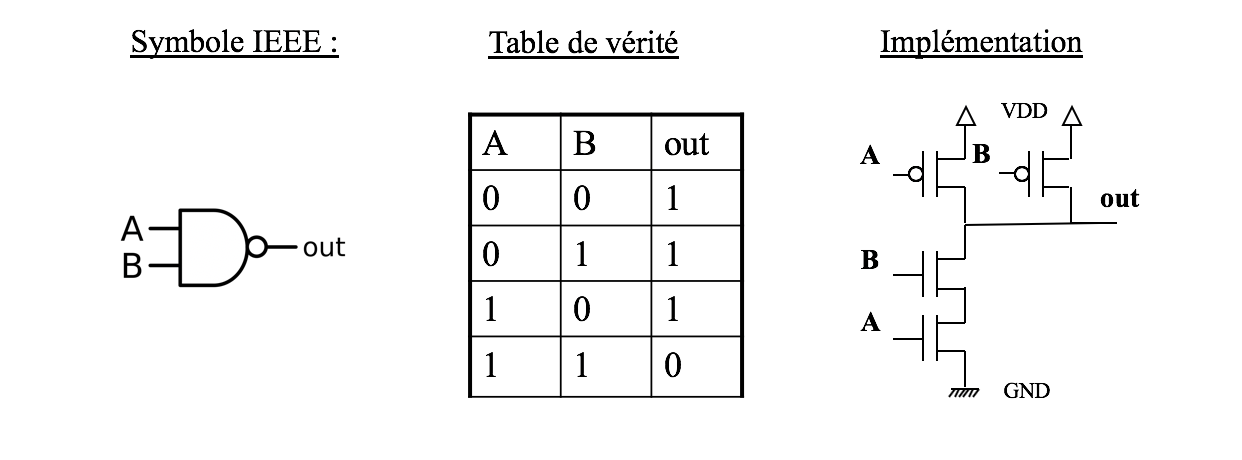
-
Porte NOR (NON OU).