1. Introduction
Il existe plusieurs façons d’aborder la notion d’itération en algorithmique et dans la plupart des langages de programmation :
-
avec des boucles (
while,for,loop, etc.) -
avec la récursivité
Nous apprendrons dans ce cours comment concevoir une solution récursive pour un problème.
|
Une recursive_fonctionion est qualifiée de récursive si elle s’appelle elle-même. |
def recursive_fonction(n):
if n>0:
recursive_fonction(n-1)
print(n)
recursive_fonction(3)
0
1
2
32. Définition
La récursivité est une démarche qui fait référence à l’objet même de la démarche à un moment du processus. En d’autres termes, c’est une démarche dont la description mène à la répétition d’une même règle. Ainsi, les cas suivants constituent des cas concrets de récursivité :
décrire un processus dépendant de données en faisant appel à ce même processus sur d’autres données plus « simples » ;
montrer une image contenant des images similaires ;
définir un concept en invoquant le même concept ;
écrire un algorithme qui s’invoque lui-même ;
définir une structure à partir de l’une au moins de ses sous-structures.
https://fr.wikipedia.org/wiki/R%C3%A9cursivit%C3%A9
Examinons le détail de l’exécution du code de l’exemple précédant :
def recursive_fonction(n):
if n>0:
recursive_fonction(n-1)
print(n)
recursive_fonction(3)On trouve dans le code de la fonction recursive_fonction(n) un appel à elle même : recursive_fonction(n-1) : C’est donc bien une fonction récursive.
Cette fonction est appelée dans le programme principal en lui passant la valeur 3 en paramètre :
-
Etape 1 : appel de la fonction
recursive_fonction()avec le paramètren = 3:-
n > 0donc appel de la fonctionrecursive_fonction()avec le paramètren = 2
-
-
Etape 2 : appel de la fonction
recursive_fonction()avec le paramètren = 2-
n > 0donc appel de la fonctionrecursive_fonction()avec le paramètren = 1
-
-
Etape 3 : appel de la fonction
recursive_fonction()avec le paramètren = 1-
n > 0donc appel de la fonctionrecursive_fonction()avec le paramètren = 0
-
-
Etape 4 : appel de la fonction
recursive_fonction()avec le paramètren = 0-
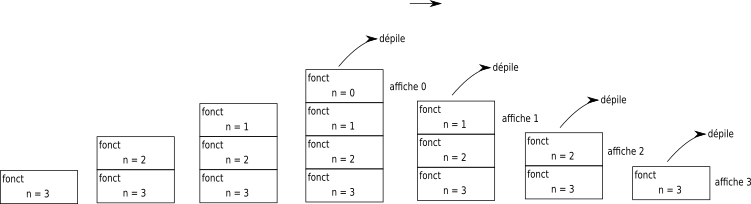
n = 0donc on exécute l’instructionprint(n)⇒ affichage :0
-
-
on "dépile" l’étape 3 (
n = 1) : on exécute l’instructionprint(n)⇒ affichage :1 -
on "dépile" l’étape 2 (
n = 2) : on exécute l’instructionprint(n)⇒ affichage :2 -
on "dépile" l’étape 1 (
n = 3) : on exécute l’instructionprint(n)⇒ affichage :3
|
Il ne faut jamais perdre de vu qu’à chaque nouvel appel de la fonction |
3. Cas simple
3.1. La factorielle
3.1.1. Définition
En mathématiques, la factorielle d’un entier naturel
nest le produit des nombres entiers strictement positifs inférieurs ou égaux àn.Cette opération est notée avec un point d’exclamation,
n!, ce qui se lit soit « factorielle de n », soit « factorielle n » soit « n factorielle ». Cette notation a été introduite en 1808 par Christian Kramp.
https://fr.wikipedia.org/wiki/R%C3%A9cursivit%C3%A9
-
\(10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3628800 \)
-
\(9! = 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 362880 \)
On constate immédiatement que l’on pourait écrire :
-
\(10! = 10 \times 9! \)
Soit en généralisant :
-
\(n! = n \times (n-1)! \)
3.1.2. Codage
Apparait alors clairement un appael récursif à la fonction factorielle, ce qui peut donc se coder de la manière suivante :
def factorielle(n):
if n>0:
return n*factorielle(n-1)
return 1|
On constate qu’une fonction récursive comporte :
|
3.1.3. Travail à faire : Factorielle
-
Coder la fonction factorielle et testez la pour les valeurs :
-
\(3! = 6 \)
-
\(5! = 120 \)
-
\(10! = 3628800 \)
-
\(100! = 9,3326 \times 10^{157} \)
-
\(1000! = 10^{2568} \)
-
|
3.2. Puissance n d’un entier positif
3.2.1. Définition
Soient \( a>0 \) et \( n \geq 0 \), la puissance \( n \)ième de \( a \) est définie par :
-
pour \( n=0 \) : \( a^{0} = 1 \)
-
pour \( n > 0 \) : \( a^{n} = a \times a^{n-1} \)
3.2.2. Codage
Cette définition mathématique comporte :
-
un point de départ \( n=0 \) pour lequel on a directement le résultat \( a^{0} = 1 \)
-
un calcul de la puissance \( n \)ième de \( a \) qui fait appel au calcul de la puissance \( (n-1) \)ième de a.
def puissance(a,n):
# cas d'arrêt
if(____):
return __
# cas récursif
return a * puissance(a,n-1)3.2.3. Travail à faire : Puissance
-
Coder la fonction
puisssance(a, n)et testez la pour les valeurs :-
\(2^{4} = 16 \)
-
\(5^{3} = 125 \)
-
\(10^{4} = 10000 \)
-
\(1000^{100} = 10^{300} \)
-
\(2^{1000} = 1,071508607 \times 10^{301} \)
-
|
3.3. Produit de deux nombres entiers positifs
3.3.1. Définition
Soient \( a \geq 0 \) et \( b \geq 0 \), le produit de \( a \) par \( b \) est définie par \( b \) fois la somme de \( a \) avec lui-même :
-
pour \( a=5 \) et \( b=3 \) : \( a \times b = 5 + 5 + 5 \) soit \( a \times b = 5 + 5 \times 2 \)
-
pour \( a=3 \) et \( b=5 \) : \( a \times b = 3 + 3 + 3 + 3 + 3\) soit \( a \times b = 3 + 3 \times 4 \)
-
pour \( a \) et \( b \) : \( a \times b = a + a \times (b-1) \)
3.3.2. Codage
Cette définition mathématique comporte :
-
un point de départ \( a = 0 \) ou \( b = 0 \) pour lequel on a directement le résultat \( a \times b = 0 \)
-
un calcul du produit de \( a \) par \( b \) qui fait appel au calcul de la somme de \( (a) \) avec le produit de \( (a) \) par \( (b-1) \).
3.3.3. Travail à faire : Produit
-
Coder la fonction
produit(a, b)et testez la pour les valeurs :-
\(2 \times 4 = 8 \)
-
\(5 \times 3 = 15 \)
-
\(10 \times 4 = 40 \)
-
\(1000 \times 100 = 100000 \)
-
\(100 \times 10000 = 100000 \)
-
4. Conception d’une fonction récursive
|
Pour écrire une fonction récursive :
|
4.1. Execices autocorrigés
-
Quelle est la sortie de cet extrait de code :
def g(n):
if(n==0):
return 1
return n * g(n+1)
print(g(3))-
Quelle est la sortie de cet extrait de code :
def h(n):
if(n==0):
return 1
return n * h(n)-1
print(h(3))-
Quelle est la sortie de cet extrait de code :
def p(n):
if(n==0):
return 1
return n * p(n-2)
print(p(3))-
Quelle est la sortie de cet extrait de code :
def h(n):
if(n==0):
return 1
return n * h(n-1)
print(h(3))5. Problème du domaine de défintion
5.1. Retour sur la fonction factorielle
on peut écrire cette fonction de cette manière :
def factorielle(n):
if n==0:
return 1
return n*factorielle(n-1)
print(factorielle(3))l’écriture d’une fonction récursive en Python s’impose d’elle même en suivant la définition mathématique avec :
-
un cas d’arrêt de la récursivité : si \( n=0 \) le résultat est \( 1 \)
-
un cas de calcul récursif : \( n \geq 0 \) pour calculer la factorielle de \( n \), on doit multiplier \( n \) avec le résultat du calcul de la factorielle \( n-1 \) (sous-problème de taille réduite)
5.2. Travail à faire : Test de la fonction factorielle
-
Coder et tester la fonction factorielle dans les cas suivants :
-
\( 0! \)
-
\( 5! \)
-
\( -5! \)
-
5.3. Gestion des valeurs négatives
|
Il ne semble pas judicieux de tester à chaque appel récursif si \( n < 0 \). Si \( n < 0 \) dés le départ il faut signaler l’erreur de domaine, mais si \( n \geq 0 \), le calcul permettra à \( n \) d’atteindre la valeur \( 0 \) (et donc arrêter le calcul) avant une valeur négative. |
|
On va séparer la vérifcation du domaine de validité de l’argument du calcul proprement dit quand l’argument est correct. |
def factorielle_argument_valide(n):
# tester si l'argument est positif ou nul pour faire les calculs
if(n < 0):
print('Pour n =', n, ', qui est négatif, factorielle(',n,') est non définie')
else:
if(n == 0):
print('Pour n =', n, ', factorielle(',n,') est égal à :', 1)
return 1
resultat = n * factorielle_argument_valide(n-1)
print('Pour n =', n, ', factorielle(',n,') est égal à :', resultat)
return resultat
factorielle_argument_valide(-5)6. Suite de Finobacci
6.1. Définition
En mathématiques, la suite de Fibonacci est une suite d’entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent.
Elle commence par les termes 0 et 1 (on trouve des définitions qui la font commencer avec 1 et 1).
Les termes de cette suite sont appelés nombres de Fibonacci
\( F_{0} \) \( F_{1} \) \( F_{2} \) \( F_{3} \) \( F_{4} \) \( F_{5} \) \( F_{6} \) \( F_{7} \) … \( F_{n} \) 0
1
1
2
3
5
8
13
\( F_{n-2} + F_{n-1} \)
https://fr.wikipedia.org/wiki/Suite_de_Fibonacci
6.2. Travail à faire : Codage de la fonction Fibonacci
-
Coder et tester la fonction
Fibonacci(n)pour tout \( n \geq 0 \).
7. Une suite quelconque
7.1. Définition
Soit la suite qui, étant donné un entier \( n \geq 0 \), calcule \( U_{n} \), le \(n_{ième} \) terme de la suite définie par
-
\( U_{0} = 2 \)
-
\( U_{n+1} = \frac{1 + 3 × U_{n}}{3 + U_{n}} \)
7.2. Travail à faire : Codage de la fonction suite
-
Coder et tester la fonction
suite(n)pour tout \( n \geq 0 \). -
Calculer \( U_{n} \) pour \( n = 0 \: à \: 20 \)
Correction |
8. PGCD
8.1. Définition
En arithmétique élémentaire, le plus grand commun diviseur ou PGCD de deux nombres entiers non nuls est le plus grand entier qui les divise simultanément.
Par exemple, le PGCD de 20 et de 30 est 10, puisque leurs diviseurs communs sont 1, 2, 5 et 10.
https://fr.wikipedia.org/wiki/Plus_grand_commun_diviseur
8.2. Travail à faire : Codage de la fonction pgcd
-
Coder et tester la fonction
pgcd(a, b)pour tout entier \( a > 0 \) et \( b > 0 \) tel que :-
pgcd(a,b) = asia = b -
sinon
pgcd(min(a,b),|a-b|)
-
-
Calculer le PGCD de :
-
\( 15 \) et \( 21 \)
-
\( 11 \) et \( 19 \)
-
\( 24 \) et \( 48 \)
-
Correction |
9. Les tours de Hanoï
9.1. Présentation
L’exemple présenté le plus souvent comme le plus percutant sur la récursivité est le problème dit des Tours de Hanoï car la solution récursive est logique, concise, élégante et … la seule viable !
C’est un jeu dans lequel on dispose de trois tours TOUR1, TOUR2 et TOUR3 et de disques troués en leur centre et de tailles différentes deux à deux.
-
Au départ, les \( n \) disques sont empilés sur la tour TOUR1 de telle sorte que chaque disque ait un diamètre inférieur au disque immédiatement en dessous de lui.
-
Ainsi, le plus grand disque de la tour se situe à sa base et le plus petit sur son sommet.

L’objectif du jeu est de déplacer tous les disques de la tour TOUR1 vers la tour TOUR3 en s’aidant uniquement de la tour TOUR2, tout en respectant les règles suivantes :
-
On ne déplace qu’un seul disque à la fois
-
Un disque ne peut pas être mis sur un disque plus petit
-
À chaque étape, la règle d’organisation des tours décrite précédemment doit être respectée.
9.2. Travail à faire : A vous de jouer !
9.3. Travail à faire : Algorithme gagnant
Pour trouver les déplacements à effectuer en un minimum de coups, il vaut mieux penser récursivement la solution au problème, quel que soit le nombre \(n \) de disques.
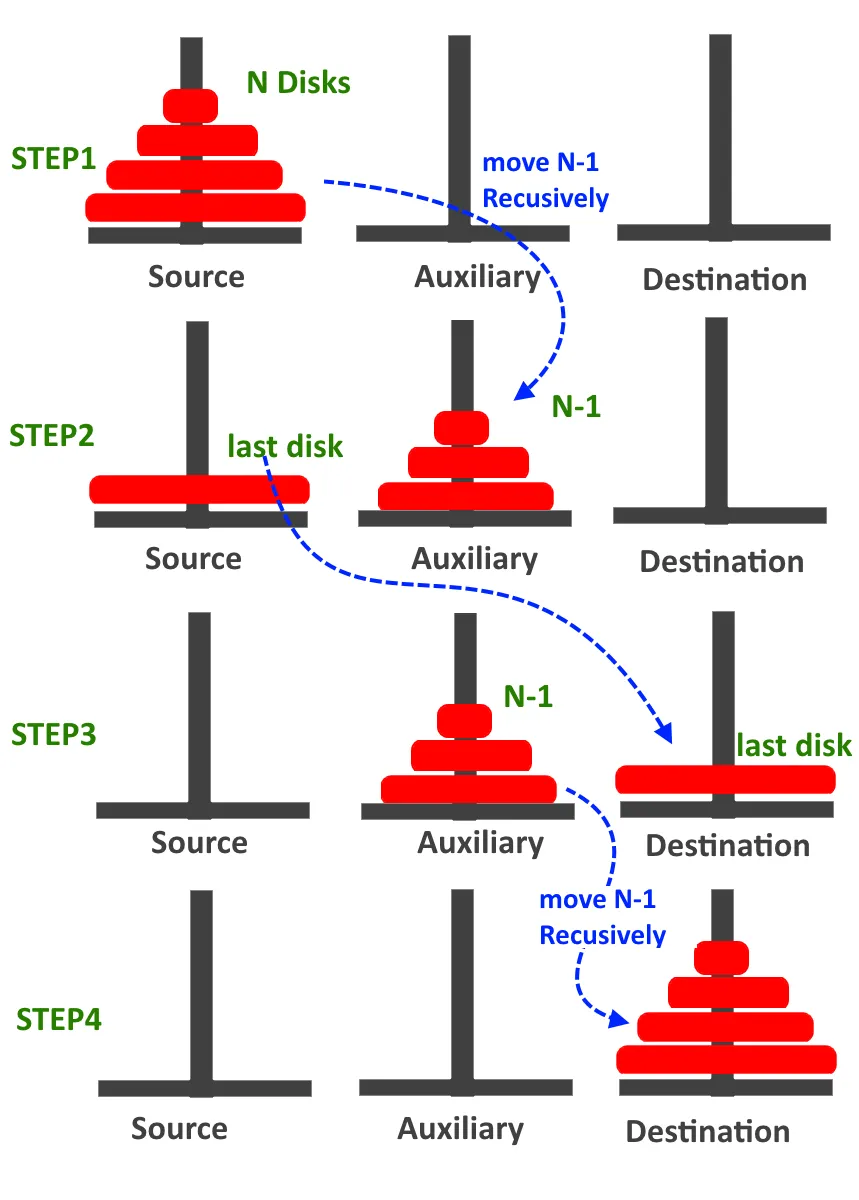
Pour déplacer \(n \) disques de la tour TOUR1 vers la tour TOUR3 en passant par TOUR2, il faudra :
-
Déplacer \(n-1 \) disques de TOUR1 vers TOUR2 en passant par TOUR3
-
Puis déplacer 1 disque de TOUR1 vers TOUR3
-
Puis déplacer(n-1) disques de TOUR2 vers TOUR3 en passant par TOUR1.
Et c’est tout…
-
Compléter le code de la fonction
hanoi(n, tour_depart, tour_arrivee , tour_intermediaire)ounest le nombre de disque(s) à déplacer -
Tester les déplacements obtenus pour 3 et 4 disques :
def hanoi(n, tour_depart, tour_arrivee , tour_intermediaire):
# Afficher le déplacement quand il n'y a qu'un disque à déplacer
if n==1:
print("Déplacer un disque de ",tour_depart," vers ",tour_arrivee)
return
# Déplacer n-1 disques de tour_depart vers tour_intermediaire en passant par tour_arrivee
???
# Déplacer 1 disques de tour_depart vers tour_arrivee
???
# Déplacer n-1 disques de tour_intermediaire vers tour_arrivee en passant par tour_depart
???
hanoi(4, 'TOUR1', 'TOUR2', 'TOUR3')10. Fonctions récursives sur les listes
10.1. Introduction
Une solution récursive est particulièrement adaptée quand on doit traiter des structures de données récursives.
Les listes qu’on appelle chaînées sont des structures récursives. En effet, on peut dire d’une liste qu’elle est :
-
soit vide
-
soit construite à partir d’un élément et d’une autre liste (ajout d’un élément dans la liste).
On peut donc en déduire que le traitement d’une liste suivra (le plus souvent) le schéma récursif suivant :
-
La liste vide correspondra au cas d’arrêt (cas trivial, de base)de la récursivité.
-
La liste résultant de l’ajout de l’élément
elementà la listereste_listecorrespondra au cas de calcul récursif avec la taille du problème diminuée si on fait le traitement surreste_liste.
|
Jusqu’à présent, quand nous avons traité des listes, nous avons le plus souvent parcouru toute la liste, élément par élément pour faire le traitement adéquat. Suivant le modèle de solution choisi, le parcours des listes pouvait se faire :
Pour la construction et le traitement récursif des listes, il est généralement admis de faire le parcours de gauche à droite. |
10.2. Démarche
|
10.3. Exemple : Nombre d’élément d’une liste
10.3.1. Définition
On cherche à écrire la fonction récursive longueur_liste() qui donne le nombre d’éléments d’une liste.
-
Cas d’arrêt :
-
la liste est vide : on retourne 0.
-
-
Cas récursif :
-
la liste n’est pas vide : on retourne la longueur de la liste privée d’un élément (par exemple, le 1er) + 1
-
10.3.2. Codage de la fonction longueur_liste
def longueur_liste ( liste ):
if( liste == []):
return 0
return 1 + longueur_liste( liste [1:])10.3.3. Travail à faire : Test de la fonction longueur_liste
-
Coder la fonction
longueur_listeet testez la pour les listes :-
[1, 2, 3, 4]
-
['a', 'b', 'c', 'd', 'e']
-
[[[1,2,3,4], ['a','b','c','d','e']]
-
[(1, 2), [1, 2], 1, 'a']
-
Correction |
10.4. Exercices
10.4.1. Travail à faire : Somme des éléments d’une liste
-
Compléter la fonction récursive
somme(liste)qui, étant donnée une liste d’entiers, calcule la somme des éléments de la liste :-
Cas d’arrêt : la liste est vide ⇒ on retourne 0
-
Cas récursif : la liste n’est pas vide ⇒ on retourne le premier élément de la liste + la somme de la liste privée du premier élément.
-
def somme(liste):
if ???:
return ???
return liste[???] + somme(liste[???])-
Tester la fonction
somme(liste)avec les listes suivantes :-
[1, 2, 3, 4]
-
[1, 10, 100, 1000]
-
[-1, 1, -2, 2, -3, 3]
-
[1, -2, 3, -4]
-
-
La fonction n’est définie que pour des listes d’entiers. Coder le test de la validité de la liste passée en paramètre à l’aide de la fonction
isinstance()qui retourne un booléen. La fonctionsomme(liste)doit retournée 0 si la liste n’est pas uniquement composée d’entiers :
all(isinstance(n, int) for n in liste)-
Tester la fonction
somme(liste)avec les listes suivantes :-
[1, 2, 3, 4]
-
['a', 'b', 'c', 'd', 'e']
-
Correction |
10.4.2. Travail à faire : Produit des éléments d’une liste
-
Coder la fonction récursive
produit(liste)qui, étant donnée une liste d’entiers, calcule le produit des éléments de la liste : -
Tester la fonction
produit(liste)avec les listes suivantes :-
[1, 2, 3, 4]
-
[1, 10, 100, 1000]
-
[-1, 1, -2, 2, -3, 3]
-
[1, -2, 3, -4]
-
-
La fonction n’est définie que pour des listes d’entiers. Coder le test de la validité de la liste passée en paramètre à l’aide de la fonction
isinstance()qui retourne un booléen. La fonctionproduit(liste)doit retournée 0 si la liste n’est pas uniquement composée d’entiers :
all(isinstance(n, int) for n in liste)-
Tester la fonction
produit(liste)avec les listes suivantes :-
[1, 2, 3, 4]
-
['a', 'b', 'c', 'd', 'e']
-
Correction |
10.4.3. Travail à faire : Nombre d’occurence dans une liste
-
Coder la fonction récursive
nb_occurrences(valeur, liste)qui, étant donnée une liste, calcule le nombre d’occurence de l’élémentvaleurde la liste : -
Tester la fonction
nb_occurrences(valeur, liste)avec les listes et les valeurs suivantes :-
On recherche le nombre de
1dans [1, 2, 3, 4, 1] -
On recherche le nombre de
'a'dans ['a', 'a', 'a', 'b', 'c', 'd', 'e', 'a']
-
Correction |
10.4.4. Travail à faire : Palindrome
Le palindrome (substantif masculin), du grec πάλιν / pálin (« en arrière ») et δρόμος / drómos (« chemin, voie »), aussi appelé palindrome de lettres, est une figure de style désignant un texte ou un mot dont l’ordre des lettres reste le même qu’on le lise de gauche à droite ou de droite à gauche, comme dans la phrase « Ésope reste ici et se repose » ou encore « La mariée ira mal » à un accent près.
Il est communément admis que l’on ne tient pas compte des signes diacritiques (accents, trémas, cédilles) ni des espaces.
https://fr.wikipedia.org/wiki/Palindrome
-
Coder la fonction récursive
palindrome(phrase)qui, étant donnée une phrase écrite sans accents ni espaces, retourne vrai si c’est un palindrome, faux sinon : -
Tester la fonction
palindrome(phrase)avec les phrases suivantes :-
p1 = "eluparcettecrapule" -
p2 = "esoperesteicietserepose" -
p3 = "engagelejeuquejelegagne" -
p4 = "cecinestpasunpalindrome"
-
Correction partielle |
