1. Représentation des entiers naturels

1.1. Pincipe

Il faut comprendre qu’un nombre peut s’exprimer de différentes manières selon le contexte et les besoins.

1.1.1. Compter en base 10

C’est notre manière naturelle de compter et de représenter les nombres.

La base 10 s’appelle aussi le décimal.

Le principe du comptage consiste à faire des paquets de 10.

Les chiffres ou digits sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

  • 9+1 est égal à 1 paquet de 10 \((10^1)\) et il reste 0.

  • 99+2 est égal à 10 paquets de 10 \((10^2)\) et il reste 1.

Un nombre décimal peut donc s’écrire sous forme de puissance de 10 de la manière suivante :

\(a_n \times 10^n + a_{n-1} \times 10^{n-1} + \ldots +a_1 \times 10^1 + a_0 \times 10^0\) avec \(a_{i} \in [0,1,2,3,4,5,6,7,8,9]\)

1.1.2. Compter en base 16

La base 16 s’appelle aussi l’hexadécimal.

C’est la base de comptage souvent utilisée pour manipuler les adresses mémoire d’un ordinateur, les adresses des interfaces réseaux, ou pour manipuler des valeurs de registre de composant électronique.

Le principe du comptage consiste à faire des paquets de 16.

Les chiffres ou digits sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. A vaut 10, B vaut 11, …​, F vaut 15.

  • 9+1 = A.

  • A+3 = D.

  • F+1 est égal à 1 paquet de 16 \((16^1)\) et il reste 0, donc \(10_{|16}\).

  • FF+2 est égal à 16 paquets de 16 \((16^2)\) et il reste 1, donc \(101_{|16}\)

Un nombre hexadécimal peut donc s’écrire sous forme de puissance de 16 de la manière suivante :

\(a_n \times 16^n + a_{n-1} \times 16^{n-1} + \ldots +a_1 \times 16^1 + a_0 \times 16^0\) avec \(a_{i} \in [0,1,2,3,4,5,6,7,8,9,10(A),11(B),12©,13(D),14(E),15(F)]\)

1.1.3. Travail faire : Addition en hexadécimal

Quel résultat des additions suivantes :

  • \(256_{|16}\) + \(DAA_{|16}\)

  • \(EF86_{|16}\) + \(6C39_{|16}\)

  • \(40AE_{|16}\) + \(236A_{|16}\)

  • \(D83B_{|16}\) + \(68A6_{|16}\)

1.1.4. Compter en base 2

La base 2 s’appelle aussi le binaire. C’est la base de comptage souvent utilisée pour manipuler des valeurs de registre de composant électronique, pour effectuer des calculs de sous-réseaux informatique, dans le cadre du développement de systèmes électroniques.

Le principe du comptage consiste à faire des paquets de 2.

Les chiffres ou digits sont 0, 1. Cette information est appelée bit (compression des mots anglais binary digit)

  • 1+1 est égal à 1 paquet de 2 \((2^1)\) et il reste 0, donc \(10_{|2}\).

  • 11+1 est égal à 2 paquets de 2 \((2^2)\) et il reste 0, donc \(100_{|2}\).

Un nombre binaire peut donc s’écrire sous forme de puissance de 2 de la manière suivante :

\(a_n \times 2^n + a_{n-1} \times 2^{n-1} + \ldots +a_1 \times 2^1 + a_0 \times 2^0\) avec \(a_{i} \in [0,1]\)

1.1.5. Travail faire : Addition en binaire

Quel résultat des additions suivantes :

  • \(11011101_{|2}\) + \(1101_{|2}\)

  • \(10010_{|2}\) + \(1110_{|2}\)

  • \(111000_{|2}\) + \(100110_{|2}\)

  • \(11111_{|2}\) + \(10101_{|2}\)

1.1.6. Compter en base 8

La base 8 s’appelle aussi l'octale. C’est la base de comptage souvent utilisée pour manipuler les droits dans le système de fichiers Linux.

Le principe du comptage consiste à faire des paquets de 8.

Les chiffres ou digits sont 0, 1, 2, 3, 4, 5, 6, 7.

  • 7+1 est égal à 1 paquet de 8 \((8^1)\) et il reste 0, \(10_{|8}\).

  • 77+2 est égal à 8 paquets de 8 \((8^2)\) et il reste 1, donc \(101_{|8}\).

Un nombre octal peut donc s’écrire sous forme de puissance de 16 de la manière suivante :

\(a_n \times 8^n + a_{n-1} \times 8^{n-1} + \ldots +a_1 \times 8^1 + a_0 \times 8^0\) avec \(a_{i} \in [0,1,2,3,4,5,6,7]\)

1.1.7. Convertir de la base 2 vers la base 16

En programmation des systèmes numériques, il arrive souvent qu’on paramètre des composants électroniques.

Les registres des composants sont le plus souvent composés de 8 ou 16 bits, chaque bit pouvant avoir une signification différente.

Afin de connaître la valeur globale à paramétrer dans le registre selon nos besoins, il faut définir les valeurs de chaque bit en s’aidant de la documentation du composant ; on obtient alors une valeur en binaire.

Les langages de programmation n’acceptent pas le binaire car l’écriture des nombres dans cette base n’est pas pratique car trop long.

L’hexadécimal est en revanche très utilisé car l’écriture des nombres est réduite et le passage au binaire est très facile.

Pour cette raison, il faut savoir passer du binaire à l’hexadécimal et inversement.
Méthode

Soit la valeur binaire : \(10100101_{|2}\) sur 8 bits. Le bit le plus à gauche est appelé le MSB (Most Significant Bit), celui le plus à droite le LSB (Less Significant Bit).

A partir du LSB, faire des groupes de 4 bits (quartets) : \(1010 0101_{|2}\).

Convertir chaque quartet en hexadécimal : \(1010_{|2}\) correspond à \(A_{|16}\) et \(0101_{|2}\) correspond à \(5_{|16}\).

Donc, la valeur hexadécimale correspondant à \(10100101_{|2}\) est \(A5_{|16}\).

1.1.8. Convertir de la base 16 vers la base 2

On fait tout simplement l’inverse :

Méthode

On convertie en binaire sur 4 bits chaque digit hexadécimal.

Exemple

\(F35A_{|16} \Leftrightarrow 1111 \quad 0011 \quad 0101 \quad 1010_{|2}\)

1.1.9. Convertir de la base 8 vers la base 2

On procède comme pour passer de l’hexadécimal au binaire mais on fait des paquets de 3 bits:

Méthode

On convertie en binaire sur 3 bits chaque digit octal.

Exemple

\(7251_{|8} \Leftrightarrow 111 \quad 010 \quad 101 \quad 001_{|2}\)

1.1.10. Convertir de la base 10 vers la base 2

Nous nous exprimons souvent en décimal car c’est le plus naturel pour nous.

Selon les travaux à réaliser nous aurons besoin de la correspondance en base 2.

Exemple à propos des réseaux informatiques :

Lorsqu’on veut découper un réseau ayant pour masque 255.255.128.0, on doit modifier ce masque en ajoutant des bits à 1 selon le nombre de sous réseaux désirés. Pour découper 2 sous-réseaux, il faut ajouter 1 bit à 1, pour le découper en 8 sous-réseaux, il faut ajouter 3 bits à 1 \((8 = 2^3)\). Pour y arriver de manière fiable, il faut convertir le masque en binaire.

Méthode

On effectue la division entière du nombre à convertir jusqu’à ce que le dividande soit égale à \(0\) ou \(1\). Les restes des divisions correspondent à la représentation binaire du nombre :

exemple

Convertir le nombre \(77\) en binaire

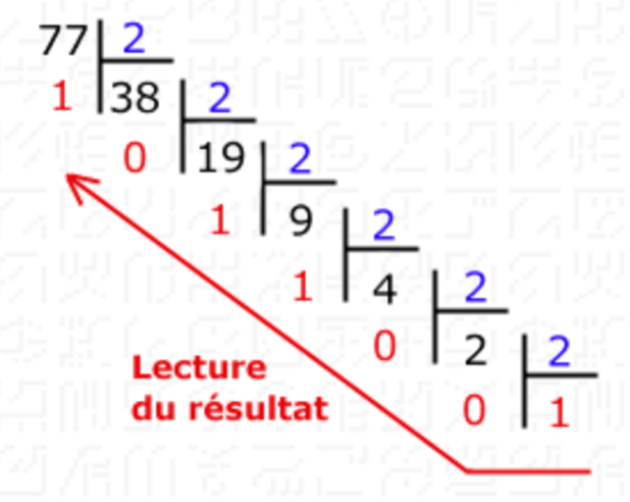
imageDivSucc

Donc, la représentation binaire de \(77_{|10}\) est \(1001101_{|2}\).

Remarque

Un nombre binaire peut s’écrire sous forme de puissance de 2 de la manière suivante :

\(a_n \times 2^n + a_{n-1} \times 2^{n-1} + \ldots +a_1 \times 2^1 + a_0 \times 2^0\) avec \(a_{i} \in [0,1]\)

Ils sont souvent représentés sous la forme d’un octet, c’est à dire un paquet de 8 bits. Dans ce cas, on peut écrire le nombre sous forme de puissance de 2 de la manière suivante :

\(a_7 \times 2^7 + a_6 \times 2^6 + a_5 \times 2^5 + a_4 \times 2^4 + a_3 \times 2^3 + a_2 \times 2^2 + a_1 \times 2^1 + a_0 \times 2^0\) avec \(a_{i} \in [0,1]\)

Soit :

\(a_7 \times 128 + a_6 \times 64 + a_5 \times 32 + a_4 \times 16 + a_3 \times 8 + a_2 \times 4 + a_1 \times 2 + a_0 \times 1\) avec \(a_{i} \in [0,1]\)

On utilise alors un tableau de conversion.

Table 1. Exemple : convertir 77 en binaire
128 64 32 16 8 4 2 1

0

1

0

0

1

1

0

1
\$77 = (0 \times 128) + (1 \times 64) + (0 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1)\$

Donc, la représentation binaire de \(77_{|10}\) est \(01001101_{|2}\) sur un octet. Le \(0\) de gauche (MSB) est non-significatif et peut donc être omis.

1.1.11. Convertir de la base 2 vers la base 10

On fait tout simplement l’inverse. La méthode la plus simple étant de preprendre le tableau de conversion.

Table 2. Exemple : convertir \(11010001_{|2}\) en décimal
128 64 32 16 8 4 2 1

1

1

0

1

0

0

0

1
\$(1 \times 128) + (1 \times 64) + (0 \times 32) + (1 \times 16) + (0 \times 8) + (0 \times 4) + (0 \times 2) + (1 \times 1) = 209_{|10}\$

1.1.12. Travail à faire : Conversions

Démarrer le Quizz :

1.2. Conversions de base en Python

1.2.1. Affichage d’un entier dans une base

En Python (comme pour tout les langages de programmation), il est très facile d’obtenir la représentation d’un entier en base 2, 10 ou 16.

Pour cela, on peut utiliser la méthode format sur les chaînes de caractères. Cette méthode permet de transformer une chaîne de caractères en remplaçant chaque champs de remplacement (sous-chaîne entourée d’accolades {}) par un des arguments de la fonction potentiellement transformé pour correspondre à un format donné.

Par exemple, le code suivant :

"Décimal: {0:d}; Hexadécimal: {0:x}; Binaire: {0:b}".format(42)

permet d’obtenir la représentation de 42 en décimal, hexadécimal et binaire. Le nombre avant les deux points dans les accolades correspond au numéro du paramètre de l’appel de la méthode format alors que la chaîne de caractères après les deux points spécifie le format voulu : d pour décimal, b pour binaire et h pour hexadécimal.

On peut aussi utiliser les fonctions bin et hex pour obtenir la représentation d’un entier en binaire ou hexadécimal.

1.2.2. Construire un entier à partir d’une représentation dans une base

Il est aussi possible en Python de créer un entier à partir d’une représentation dans une base quelconque grâce au constructeur int. Un appel int(string_base_representation, base_value) permet d’obtenir l’entier correspondant à la représentation string_base_representation en base base_value.

1.2.3. Travail à faire : Conversions

Ecrire un programme python qui permet d’obtenir :

  • la représentation en base 2 du nombre \(x=FEDCBA9876543210_{|16}\).

  • la représentation en base 16 du nombre \(y=11110000101011110111_{|2}\).

  • Que remarquez-vous entre les deux représentations des nombres \(x\) et \(y\) ?

1.2.4. Travail à faire : Additions

Complétez le programme suivant qui demande à l’utilisateur la base dans laquelle deux nombres sont fournis et calcul leur somme :

base = int(input('base (2, 10, 16) : '))
nb1 = input('nombre 1 : ')
nb2 = input('nombre 2 : ')

somme = ???
resultat = nb1 + ' + ' + nb2 +  ' = '
if (base == 2):
  resultat = resultat + ???
elif (base == 10):
  resultat = resultat + ???
elif (base == 16):
  resultat = resultat + ???

print(resultat)

2. Représentation des entiers relatifs en binaire

Un ordinateur manipule des informations stockées en mémoire.

La mémoire est organisée en groupes de 8 bits (octet) repérés par une adresse (souvent exprimée en hexadécimal).

Un octet mémoire permet de mémoriser une valeur comprise entre 0 et 255.

Comment faire pour stocker des valeurs signées négatives ?

Il serait naturel de représenter les entiers relatifs en utilisant un bit pour le signe et les autres pour la valeur absolue. Ainsi, avec des mots de 8 bits, on utiliserait 1 bit pour le signe et 7 bits pour la valeur absolue.

Cependant, il faut que l’ordinateur puisse être capable de réaliser des opérations (addition, …​) avec ces valeurs en mémoire.

Additionnons 73 et 48 en base 10 :

\(73_{|10} = 01001001_{|2} \text{ et } 48_{|10} = 00110000_{|2}\)

\(\begin{array}{cc} & 01001001 \\ + & 00110000 \\ \hline & 01111001 \\ \end{array}\)

\(01111001_{|2} = 121_{|10}\)

Les deux nombres étant positifs, tout va bien.

Additionnons maintenant 73 avec -5 : Le résultat attendu est 68.

\(73_{|10} = 01001001_{|2} \text{ et } -5_{|10} = 10000101_{|2}\)

\(\begin{array}{cc} & 01001001 \\ + & 10000101 \\ \hline & 11001101 \\ \end{array}\)

\( 11001101_{|2} = 77_{|10} \) Conclusion le codage du nombre négatif n’est pas le bon.

L’utilisation seule du bit de poid fort pour identifier le signe d’un nombre en binaire n’est pas suffisant. Il faut également coder différemment sa valeur absolue.

C’est la méthode dite du "complément à deux qui est utilisée".

2.1. Complément à deux

La plupart des langages appliquent la méthode appelée "complément à deux".

Le complément à deux ne s’applique qu’à des nombres ayant tous la même longueur :

  • codés sur \(N\) bits, les nombres binaires peuvent représenter les valeurs entières de \(-2^{N-1}\) à \(2^{N-1} - 1\).

  • Si on utilise des mots de 16 bits, on peut donc représenter les entiers relatifs compris entre -32768 et 32767.

  • Sur 16 bits, on représente un entier relatif \(r\) :

    • positif ou nul comme l’entier naturel \(x=r\)

    • strictement négatif comme l’entier naturel \(x = r + 2^{16} = r + 65 536\) avec \(r < 0\).

Ainsi, les entiers naturels de 0 à 32 767 correspondent aux entiers relatifs positifs ou nuls et les entiers naturels de 32 768 à 65 535 représentent les entiers relatifs strictement négatifs.

Il existe une manière facile de calculer la représentation de l’opposé d’un nombre représenté en complément à deux qui consiste à :

  • Convertir la valeur absolue du nombre

  • Appliquer un complément à 1 : inverser tous les bits (\(1\rightarrow 0\) et \(0\rightarrow 1\))

  • Ajouter 1 au résultat en ignorant le bit supplémentaire si on dépasse le nombre de bits fixé.

exemple : codage de -85 sur 8 bits

  • Conversion de la valeur absolue : \(85_{|10} = 01010101_{|2}\)

  • Complément à 1 : \(10101010_{|2}\)

  • Ajouter 1 : \(10101011_{|2}\)

Donc : \(-85_{|10} = 10101011_{|2}\)

Vérification : \(85 - 85 = 0\) ?

\(\begin{array}{ccc} & 0101 & 0101 \\ + & 1010 & 1011 \\ \hline \color{red}1 & 0000 & 0000 \\ \end{array}\)

En binaire signé, il est très important de connaitre le format des nombres. Ici, nous avions une représentation sur 8 bits, le neuvième bit qui apparait lors de l’opération (retenue), est tout simplement ignoré.

2.1.1. Travail à faire : Conversions

Démarrer le Quizz :

2.2. Calcul du complément à 2 en python

En python, on peut calculer le complément à deux d’un entier à l’aide de la fonction suivante :

def two_complement_representation(value: int, nb_bits: int):
    """Return the two's complement of value with nb_bits bits"""
    assert -(2 ** (nb_bits-1)) <= value < 2 ** (nb_bits-1), \
        "Value " + str(value) + " should have been between " + \
        str(-(2 ** (nb_bits-1))) + \
        " and " + str(2 ** (nb_bits-1)-1)
    return ("{0:{fill}" + str(nb_bits) + "b}").format(value % (2 ** nb_bits), fill='0')

2.2.1. Travail à faire : Conversions

  • Calculer (en Python avec la fonction ci-dessus) la représentation en complément à deux sur 16 bits de : -3, -15, -256 et -1024.

  • Vérifier à la main (à l’aide de la méthode facile pour calculer l’opposé) que la fonction donne bien le bon résultat.

  • Comment détecter rapidement à partir de la représentation binaire d’un nombre signé si celui-ci est positif ou négatif ?

  • Additionner en base 2 les nombres correspondant à la représentation en complément à deux de -15 et +16. Quel résultat obtenez-vous ?

  • Pourquoi la fonction two_complement_representation calcule bien la représentation en complément à deux de value sur nb_bits bits ?

the_end.jpg