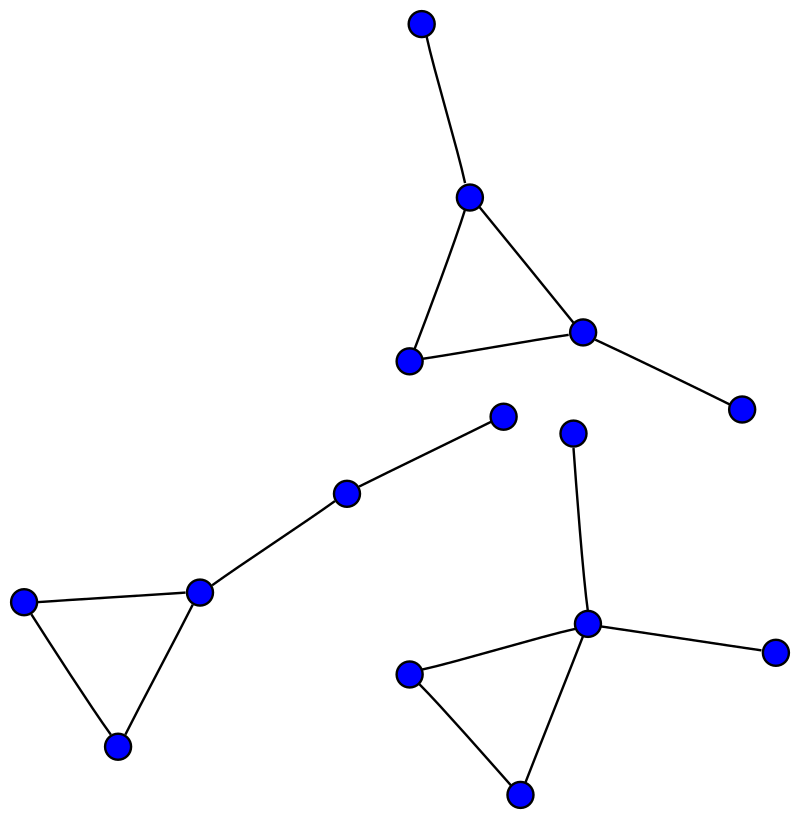
1. Description
La structure de données abstraite de graphes consiste en un ensemble fini, éventuellement mutable de sommets ou nœuds ou points, avec un ensemble de paires ordonnées ou non de tels éléments Ces paires sont des arêtes, arcs non orientés, ou lignes pour un graphe non orienté, et flèches, arêtes orientées , arcs, ou lignes orientées dans le cas orienté. Les sommets peuvent faire partie de la structure, ou être des entités extérieures, représentées par des entiers ou des références.
Une structure de graphe peut aussi associer, à chaque arête, une « valeur », telle qu’une étiquette ou une valeur numérique (un coût, une capacité, une longueur, etc.). Plus généralement, un graphe peut aussi être donnée par deux ensembles d’objets, un de sommets et un ensemble d’arêtes, muni de deux applications qui, à chaque arête, associent son sommet de départ et son sommet d’arrivée. Cette vision permet d’associer des valeurs à chaque objet (sommet ou arête).
|
Un graphe est un objet mathématique (très utilisé, notamment en informatique) constitué de sommets reliés entre eux par des arêtes : 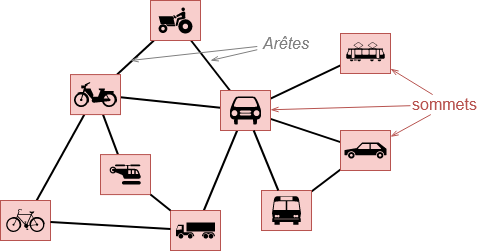
Figure 1. Exemple de graphe
|
2. Utilités
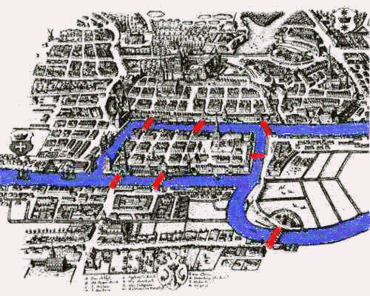
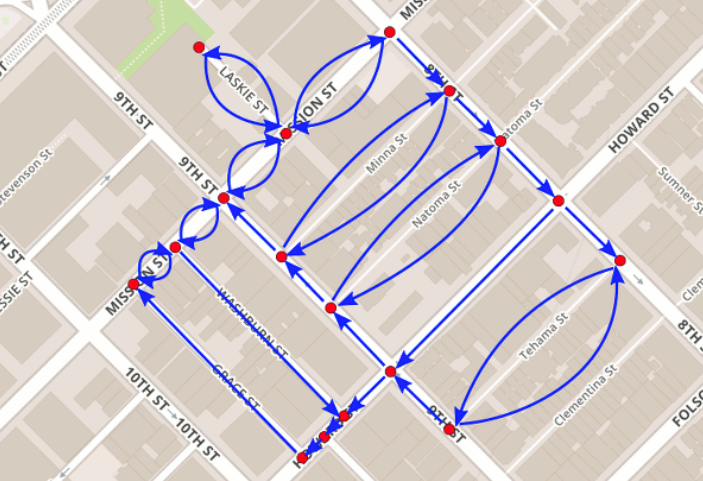
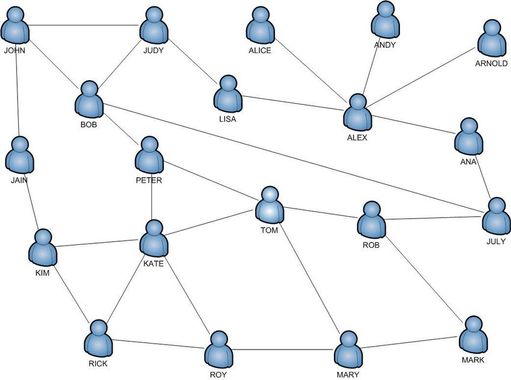
Les graphes se retrouvent dans de très nombreux domaines. Organiser une tournée de distribution de lettres, cheminement d’un colis, trajet d’une ville à un autre (train, avion, voiture, mélange de tout ça, optimiser sur le temps, sur le prix, sur le coût écologique), métro, réseaux d’ordinateur, distribution du travail à des personnels, réseaux sociaux, les liens sur les sites web. Euler serait à l’origine de la théorie des graphes en 1741 lorsqu’il pose le problème des 7 ponts de Konigsberg.
|
De manière générale :
Un graphe peut modéliser toute structure où les liens jouent un rôle aussi important que les éléments pris individuellement :
|
3. Définitions
|
On définit un graphe \(G\) par un couple \(G=(V,E)\) avec :
Chaque arête est définie par une paire de deux sommets distincts : \( E \subseteq \{\{v_1,v_2\} | (v_1,v_2) \in V^2 \land v_1 \ne v_2\}\) |
3.1. Types de graphes
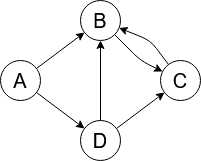
3.1.1. Graphes orientées
|
En donnant un sens aux arêtes d’un graphe, on obtient un digraphe (ou graphe orienté). Le mot « digraphe » est la contraction de l’expression anglaise « directed graph ». Un digraphe fini \(G=(V,E)\) est défini par l’ensemble fini \(V=\{v_1,v_2,…,v_n\}\) dont les éléments sont appelés sommets, et par l’ensemble fini \(E=\{e_1,e_2,…,e_m\} \) dont les éléments sont appelés arcs. Un arc \(e\) de l’ensemble \(E\) est défini par une paire ordonnée de sommets. Lorsque \(e=(u,v)\),on dit que l’arc \(e\) va de \(u\) à \(v\). On dit aussi que \(u\) est l’extrémité initiale et \(v\) l’extrémité finale de \(e\). |
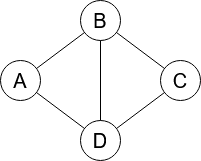
3.1.2. Graphe non orientés
|
Dans un graphe dit non orienté, l’ordre dans le couple des sommets formant les arcs est omis. La terminologie utilise alors le mot arête au lieu d’arc. Un graphe est simple si au plus une arête relie deux sommets et s’il n’y a pas de boucle sur un sommet. On peut imaginer des graphes avec une arête qui relie un sommet à lui-même (une boucle), ou plusieurs arêtes reliant les deux mêmes sommets. On appelera ces graphes des multigraphes. |
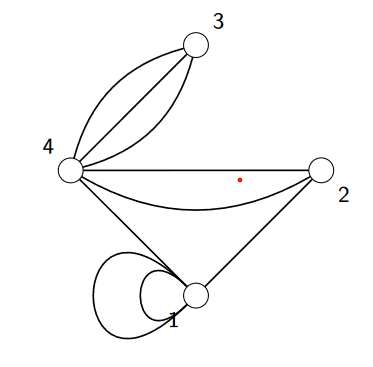
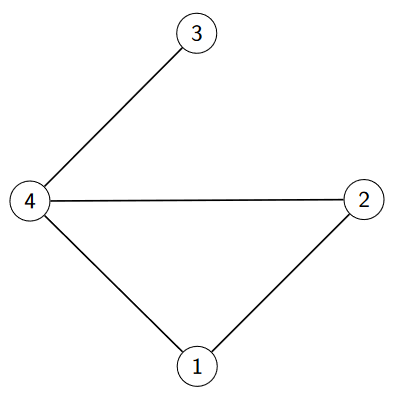
3.2. Voisinage et adjacence
|
Lorsque qu’un sommet \(v_1\) est relié à un sommet \(v_2\) par une arête, on dit que \(v_2\) est adjacent à \(v_1\), ou que \(v_2\) est un voisin de \(v_1\). |
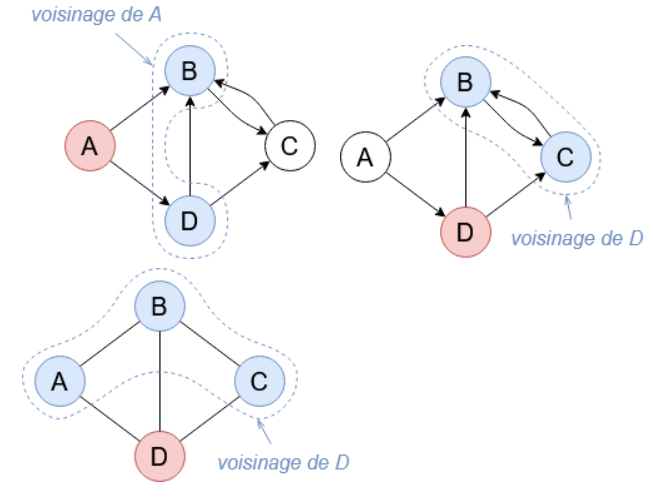
|
Adjacence
Deux arcs (ou arêtes) sont dits adjacents s’ils ont au moins une extrémité commune. |
3.2.1. Successeurs
|
Définition
On note \(\Gamma_i\) l’ensemble des successeurs du sommet \(i \in V\). |
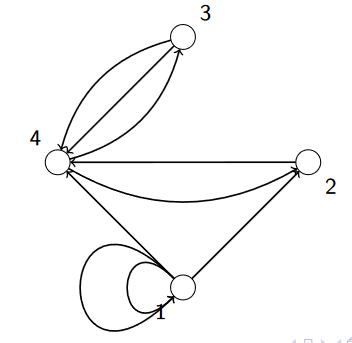
Les successeurs du sommet 1 sont :
-
Le sommet 1 lui même (2 fois)
-
Le sommet 4
-
Le sommet 2
3.2.2. Travail à faire : Trouver les successeurs
-
Qui sont les successeurs du sommet 2 ?
-
Qui sont les successeurs du sommet 4 ?
-
Qui sont les successeurs du sommet 3 ?
3.2.3. Prédecesseurs
|
Définition
On note \(\Gamma^{-1}_i\) l’ensemble des prédecesseurs du sommet \(i \in V\). |

Les prédecesseurs du sommet 1 sont :
-
Le sommet 1 lui même (2 fois)
3.2.4. Travail à faire : Trouver les prédecesseurs
-
Qui sont les prédecesseurs du sommet 2 ?
-
Qui sont les prédecesseurs du sommet 4 ?
-
Qui sont les prédecesseurs du sommet 3 ?
3.2.5. Degré et demi-degré
|
Demi-degré extérieur
Le nombre d’arcs ayant \(i\) pour extrémité initiale est appelé le demi-degré extérieur de \( i \in V \) et est noté \(d^{+}_{G}(i) \) Le demi-degré extérieur d’un sommet est donc le nombre d’arcs qui le quitte. C’est le nombre de ses successeurs |

\(d^{+}_{G}(1) = 4\) :
-
2 vers lui-même
-
1 vers le sommet 2
-
1 vers le sommet 4
3.2.6. Travail à faire : Trouver les demi-degrés extérieurs
-
Quel est le demi-degré extérieur du sommet 2 ?
-
Quel est le demi-degré extérieur du sommet 3 ?
-
Quel est le demi-degré extérieur du sommet 4 ?
|
Demi-degré intérieur
Le nombre d’arcs ayant \(i\) pour extrémité finale est appelé le demi-degré intérieur de \( i \in V \) et est noté \(d^{-}_{G}(i) \) *Le demi-degré intérieur d’un sommet est donc le nombre d’arcs qui y entre. C’est le nombre de ses prédecesseurs * |

\(d^{-}_{G}(1) = 2\) :
-
2 de lui-même
3.2.7. Travail à faire : Trouver les demi-degrés extérieurs
-
Quel est le demi-degré intérieur du sommet 2 ?
-
Quel est le demi-degré intérieur du sommet 3 ?
-
Quel est le demi-degré intérieur du sommet 4 ?
|
Degré d’un sommet
On appele le degré d’un sommet le nombre d’arêtes ou d’arcs qui le quitte ou qui y entre. C’est la somme des demi-degrés intérieur et extérieur pour le sommet \( i \) :
\$d_{G}(i) = d_{G}^{+}(i) + d_{G}^{-}(i)\$
|

-
\(d_{G}(1) = d_{G}^{+}(1) + d_{G}^{-}(1) = 6\)
3.2.8. Travail à faire : Trouver les degrés des sommets du graphe
-
Quel sont les degrés des sommets 2, 3 et 4 ?
Correction
|
3.2.9. Travail à faire : Trouver les degrés des sommets du graphe non-orienté

-
Quel sont les degrés des sommets 1, 2, 3 et 4 ?
Correction
Ce graphe est caractérisé par sa liste des degrés : |
3.2.10. Théorèmes
|
\$sum_{i=1}^{n} d(i) = 2 times A\$
avec \( A \) : nombre d’arêtes Dans un graphe simple, la somme des degrés des sommets est toujours paire. |
3.3. Matrice d’incidence
|
Une matrice d’indicence sommets-arcs \(A \in \{−1,0,+1\}^{n \times m}\) est définie par :
\[A_{i,e} =
\left\{
\begin{array}{ll}
+1 \: si \: i \: est \: l'extr\acute{e}mitr\acute{e} \: initiale \: de \: l'arc \: e \\
−1 \: si \:i \: est \: l'extrr\acute{e}mitr\acute{e} \: terminale \: de \: l'arc \: e \\
0 \: sinon
\end{array}
\right.\]
|
3.3.1. Travail à faire : Compléter la matrice d’incidence d’un graphe orienté
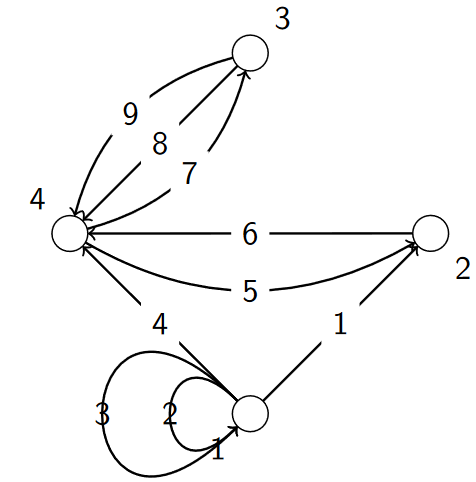
La matrice représente les arcs en colonnes et les sommets en lignes :
-
Compléter la matrice d’incidence pour les noeuds 2, 3, et 4.
Correction
\[A=
\begin{bmatrix}
1 & -1 & -1 & 1 & 0 & 0 & 0 & 0 & 0 \\
-1 & 0 & 0 & 0 & -1 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 & 1 \\
0 & 0 & 0 & -1 & 1 & -1 & 1 & -1 & -1
\end{bmatrix}\]
|
3.3.2. Cas d’un graphe non-orienté
|
Dans le cas d’un graphe non-orienté, la matrice \(A\) précédente se simplifie de la manière suivante :
\[A_{i,e} =
\left\{
\begin{array}{ll}
+1 \: si \: i \: est \: une \: extr\acute{e}mitr\acute{e} \: de \: l'ar\hat{e}te \: e \\
0 \: sinon
\end{array}
\right.\]
|
3.3.3. Travail à faire : Compléter la matrice d’incidence d’un graphe non-orienté
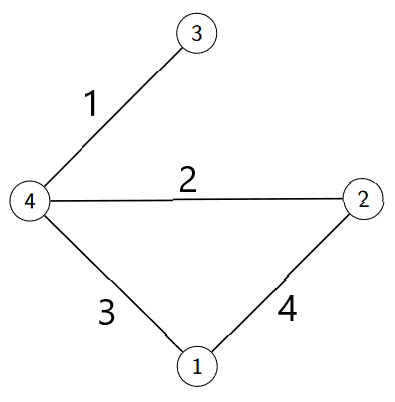
La matrice représente les arcs en colonnes et les sommets en lignes :
-
Compléter la matrice d’incidence pour les noeuds 2, 3, et 4.
Correction
\[A =
\begin{bmatrix}
0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 \\
1 & 0 & 0 & 0 \\
1 & 1 & 1 & 0
\end{bmatrix}\]
|
3.4. Matrice d’adjacences
|
Cette matrice est agalement appelée matrice d’incidence sommets-sommets. Dans le cas d’un 1-graphe (un arc unique entre deux sommets), on peut envisager une représentation sous forme d’une matrice carrée, \( A \in \{0,1\}^{n \times n} \), dite sommets-sommets ou d’adjacence. On a :
\[A_{i,e} =
\left\{
\begin{array}{ll}
+1 \: si \: les \: sommets\: i \: et \: j \: sont \: adjacents \\
0 \: sinon
\end{array}
\right.\]
|
3.4.1. Travail à faire : Compléter la matrice d’adjacences d’un graphe orienté
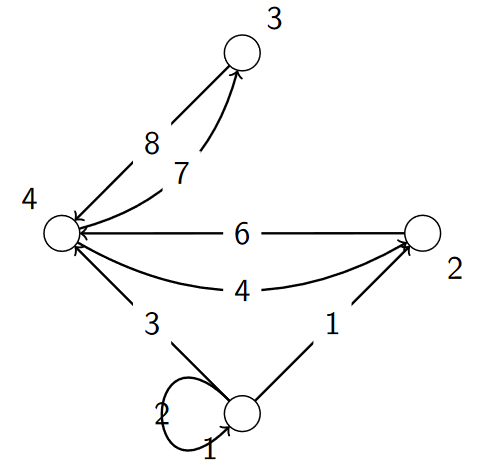
La matrice représente les connexions entre les sommets en lignes et en colonnes.
-
Les sommets de départs sont en lignes : La somme d’une ligne représente le demi-degré extérieur du sommet.
-
Les sommets d’arrivés sont en colonnes : La somme d’une colonne représente le demi-degré intérieur du sommet.
-
Compléter la matrice d’adjacences pour les noeuds 2, 3, et 4.
Correction
\[A=
\begin{bmatrix}
1 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 \\
0 & 1 & 1 & 0 \\
\end{bmatrix} \\\]
Le calcul des demi-degrés des sommets est simple :
\[d^{+}(1) = 3 \: et \: d^{-}(1)=1 \\
d^{+}(2) = 1 \: et \: d^{-}(2)=2 \\
d^{+}(3) = 1 \: et \: d^{-}(3)=1 \\
d^{+}(4) = 2 \: et \: d^{-}(4)=3 \\\]
|
3.4.2. Cas d’un graphe simple
|
Rappel : Un graphe est simple si au plus une arête relie deux sommets et s’il n’y a pas de boucle sur un sommet. Dans le cas d’un graphe simple, la matrice d’ajacence est symétrique. Elle représente les liaisons entre les sommets :
\[A_{i,e} =
\left\{
\begin{array}{ll}
+1 \: si \: les \: sommets\: i \: et \: j \: sont \: liés \\
0 \: sinon
\end{array}
\right.\]
|
3.4.3. Travail à faire : Compléter la matrice d’adjacences d’un graphe simple

La matrice représente les sommets en colonnes et en lignes :
-
Compléter la matrice d’adjacence pour les sommets 2, 3, et 4.
Correction
\[A =
\begin{bmatrix}
0 & 1 & 0 & 1 \\
1 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 \\
1 & 1 & 1 & 0
\end{bmatrix}\]
La somme d’une ligne donne le degré du sommet :
\[d(1) = 2 \\
d(2) = 2 \\
d(3) = 1 \\
d(4) = 3\]
|
4. Exercices
Le site https://graphonline.ru/fr/ permet de créer, représenter et appliquer des algorithmes à des graphes.
4.1. Exercice 1
-
Dessiner le graphe \(G= [V,A]\) défini par :
-
\(V={1,2,3,4,5}\)
-
\(A={(1,2); (2,1); (2,3); (2,3); (2,2); (5,1); (5,5); (3,4); (3,5); (4,3); (4,5)}\)
-
-
Donner les demi-degrés extérieurs et intérieurs, et les degrés de tous les sommets.
-
Donner la matrice d’adjacences du graphe.
Correction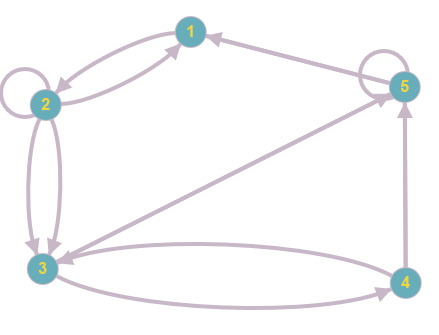
Figure 21. Représentation du graphe
Listes des demi-degrés extérieurs :
Soit \(d^{+} = [1, 4, 2, 2, 2] \) Listes des demi-degrés intérieurs :
Soit \(d^{+} = [2, 2, 3, 1, 3] \) listes des degrés de chaque sommets : Listes des demi-degrés intérieurs :
Soit \(d^{+} = [3, 6, 5, 3, 5] \)
\[A =
\begin{bmatrix}
0 & 1 & 0 & 0 & 0 //
1 & 1 & 1 & 0 & 0 //
0 & 0 & 0 & 1 & 1 //
0 & 0 & 1 & 0 & 1 //
1 & 0 & 0 & 0 & 1
\end{bmatrix}\]
Remarque : La matrice d’incidence ne permet pas de matérialiser les deux arcs existants entre les sommets 2 et 3. La matrice d’incidence serait mieux adaptée dans ce cas. |
4.2. Exercice 2
-
Dessiner le 1-graphe \(G\) pour lequel \(V=\{1,2,3,4,5\}\) et dont les successeurs de chaque sommet sont donnés par
-
\( \Gamma_1 = \{ 2 \} \)
-
\( \Gamma_2 = \{ 1,3 \} \)
-
\( \Gamma_3 = \{ 4,5 \} \)
-
\( \Gamma_4 = \{ \emptyset \} \)
-
\( \Gamma_5 = \{ 1,5 \} \)
-
-
Donner les demi-degrés extérieurs et intérieurs, et les degrés de tous les sommets.
-
Donner la matrice d’adjacences du graphe.
Correction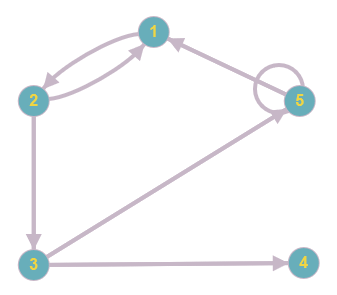
Figure 22. Représentation du graphe
Listes des demi-degrés extérieurs :
Soit \(d^{+} = [1, 2, 2, 0, 2] \) Listes des demi-degrés intérieurs :
Soit \(d^{+} = [2, 1, 1, 1, 2] \) listes des degrés de chaque sommets :
Soit \(d^{+} = [3, 3, 3, 1, 4] \)
\[A =
\begin{bmatrix}
0 & 1 & 0 & 0 & 0 //
1 & 0 & 1 & 0 & 0 //
0 & 0 & 0 & 1 & 1 //
0 & 0 & 0 & 0 & 0 //
1 & 0 & 0 & 0 & 1
\end{bmatrix}\]
Remarque : Il est fréquent qu’on représente un graphe à l’aide de sa liste des successeurs ou d’un dictionnaire de successeurs : |
4.3. Exercice 3
-
Dessiner tous les graphes simples ayant 3, 4, 5 et 6 sommets dont tous les sommets sont de degré 2
Correction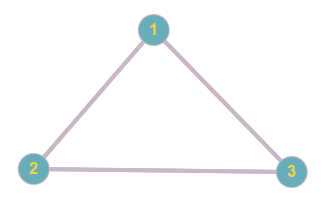
Figure 23. Graphe à 3 sommets tous de degré 2
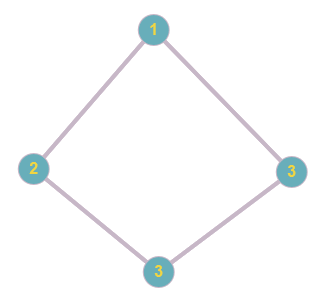
Figure 24. Graphe à 4 sommets tous de degré 2
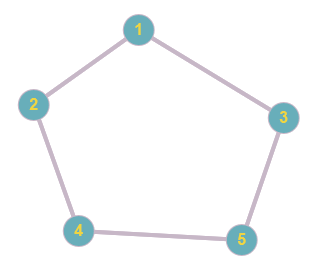
Figure 25. Graphe à 5 sommets tous de degré 2
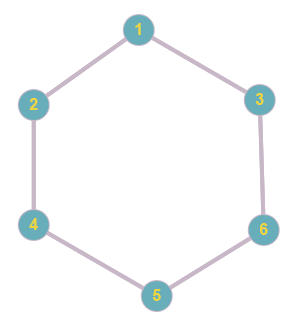
Figure 26. Graphe à 6 sommets tous de degré 2
|
4.4. Exercice 4
-
Peut-on construire un graphe de 5 sommets et 11 arêtes ?
-
Dessiner un graphe à 5 sommets avec le maximum d’arêtes.
CorrectionUn tel graphe est impossible. Le maximum d’arêtes que l’on peut dessiner est 10. 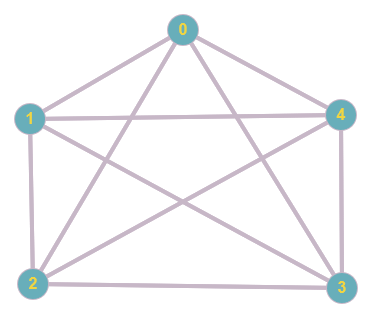
Figure 27. Graphe à 5 sommets et 10 arêtes
Remarque : Le degré maximum de chaque sommet dans dans un graphe simple à \(n\) sommets est de \( n - 1\), donc le nombre maximum d’arêtes est de \( \frac{n \times (n-1)}{2} \) |
4.5. Exercice 5
-
Une personne souhaiterait inviter six amis que nous désignons par les chiffres 1, 2, 3, 4, 5 et 6. Malheureusement, certains de ces amis ont des relations difficiles :
-
1 a des relations difficiles avec 2,
-
4 a des relations difffciles avec 5,
-
2 a des relations difficiles avec 1, 5, 6
-
5 a des relations difficiles avec 2, 3, 4, 6,
-
3 a des relations difficiles avec 5,
-
6 a des relations difficiles avec 2,5
-
-
Représenter cette situation par un graphe dans lequel 2 personnes pouvant être invitées en même temps sont reliées par une arête.
-
Chercher une clique ayant le plus grand nombre de sommets.
Remarque : une clique est un sous-graphe où tous les sommets sont adjacents (reliés entre-eux). Une clique est un sous-graphe complet.
Correction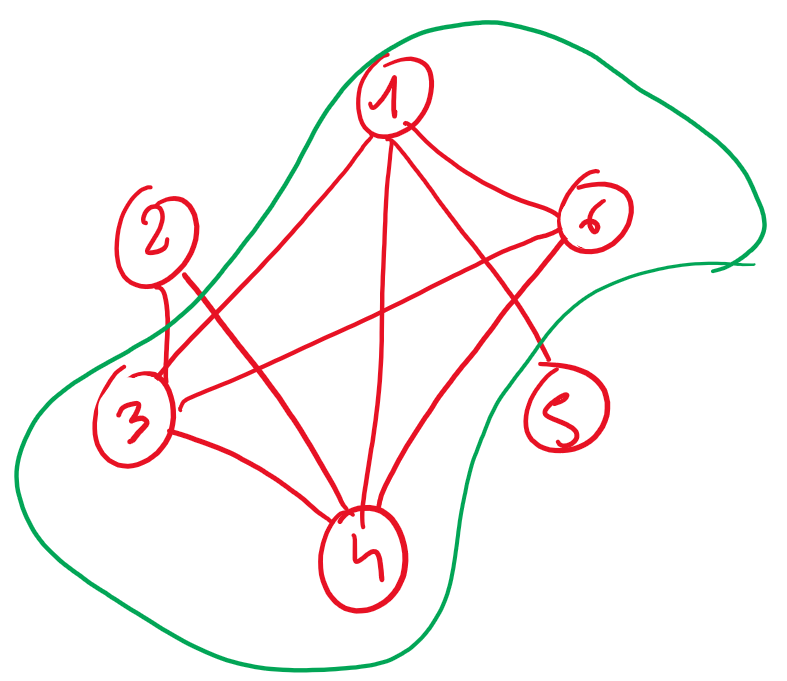
Figure 28. Graphe des amis
On peut inviter 1, 3, 4 et 6 car ils sont tous reliés entre-eux. |
4.6. Exercice 6
-
Les graphes simples dont les listes des degrés sont les suivants sont ils possibles ? Essayer de les dessiner.
-
d1 = [4,2,2,1,1] -
d2 = [2,2,1,0,0] -
d3 = [6,4,4,3,3,2,1,1]
-
Correction
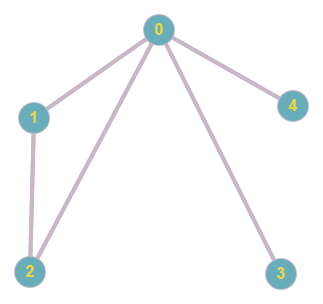
Figure 29. Graphe à partir de d1
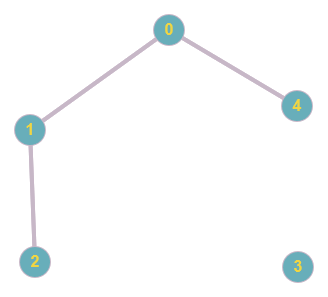
Figure 30. Graphe à partir de d2
Remarque : Un graphe ne peut pas être construit à partir de cette liste de degrés. On remarque que la somme des degrés est impaire, le graphe est irréalisable car le nombre d’arêtes est \( \frac{\sum_{i=0}^{n}d(i)}{2} \)
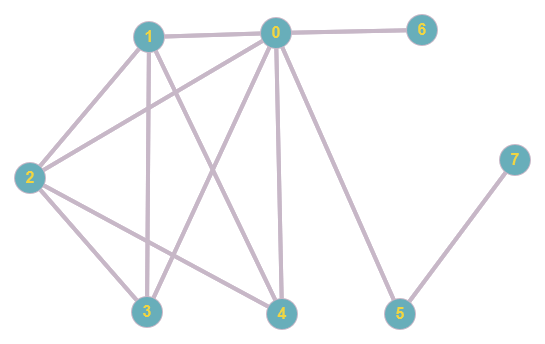
Figure 31. Graphe à partir de d3
|
4.7. Exercice 7
D’après le théorème de Havel-Hakimi, un graphe simple à \(n \) sommets est réalisable à partir de sa liste des degrés \( d \) triée dans l’ordre décroissant si et seulement le graphe simple définit par sa liste des degrés \( d' \) est réalisable avec :
On applique le théorème jusqu’à ce que l’on obtienne :
-
\( d' = 0 \) : Le graphe est réalisable
-
\( d' \ne 0 \) : Le graphe n’est pas réalisable
Explication vidéo :
-
Appliquer le théorème d’Havel-Hakimi aux graphes définits par les listes degrés suivantes :
-
\( d1 = [5,5,5,3,3,3,3,3]\)
-
\( d2 = [5,5,4,3,3,3,3,1]\)
-
\( d3 = [6,5,5,3,2,2,1,1]\)
-
\( d3 = [6,5,2,2,1,1]\)
-
5. Programmation
-
Nous utiliserons le module
networkxqui permet de facilement créer, manipuler et représenter les graphes en Python. -
Nous utiliserons la classe
Graphpour instancier l’objetG. -
Il est nécessaire de connaitre les traductions suivantes :
-
Sommet/Noeud: node
-
Arête/lien: edge
-
Graphe: graph
-
Voisins: neighbors
-
5.1. Création d’un graphe simple
-
Import des modules nécessaires :
import networkx as nx
import matplotlib.pyplot as plt # pour les représentations graphiques-
Instanciation :
G = nx.Graph()-
Ajout de sommets :
G.add_node("Paris")
G.add_node("Lyon")-
Ajout d’une arête :
G.add_edge("Paris", "Lyon")-
Dessiner le graphe avec les labels des noeuds :
nx.draw(G, with_labels=True)5.1.1. Travail à faire : Dessiner un graphe simple
-
Créer le graphe simple qui représente les liaisons routières entre les ville suivantes :
-
Villes :
-
Paris
-
Lyon
-
Marseille
-
Nice
-
Montpellier
-
Toulouse
-
Rennes
-
Nancy
-
-
Liaisons routières
-
Paris \(\leftrightarrow\) Lyon
-
Lyon \(\leftrightarrow\) Marseille
-
Nice \(\leftrightarrow\) Marseille
-
Nice \(\leftrightarrow\) Lyon
-
Montpellier \(\leftrightarrow\) Marseille
-
Montpellier \(\leftrightarrow\) Toulouse
-
Paris \(\leftrightarrow\) Toulouse
-
Rennes \(\leftrightarrow\) Toulouse
-
Rennes \(\leftrightarrow\) Paris
-
Nancy \(\leftrightarrow\) Paris
-
Nancy \(\leftrightarrow\) Lyon
-
5.1.2. Travail à faire : Créer un graphe simple
On souhaite créer un graphe simple à partir de son dictionnaire de successeurs également nommé dans le cas d’un graphe simple, dictionnaire d’adjacences ou des voisins.
-
Ecrire une classe
Graphequi comporte les attributs et les méthodes :-
Attributs :
-
voisins : dictionnaire d’adjacences
-
G: objet de la classeGraphdu modulenetworkx
-
-
Méthodes :
-
Constructeur : initialise les attributs et construit le graphe à partir de son dictionnaire d’adjacences
-
donne_voisins(sommets): donne la listes des voisins du sommetsommet -
ajoute_sommet(sommet): ajoute un nouveau sommet nommésommetau graphe -
ajoute_lien(sommet1, sommet2): ajoute un nouveau lien entre lessommet1etsommet2 -
trace(): trace le graphe
-
-
-
Créer un objet de la classe
Graphenommégraphe_des_routesinstancié à partir du dictionnaire d’adjacences du réseau routier de l’exercice précédent. -
Tracer le graphe du réseau reseau_routier.
-
Afficher la liste des voisins de "Paris"
5.1.3. Travail à faire : Degré d’un sommet
-
Ajouter à la classe
Grapheune méthodedegre(sommet)qui retourne le degré de sommetsommet
5.1.4. Travail à faire : Matrice d’adjacences
-
Ajouter à la classe
Grapheune méthodematrice_adjacences()qui retourne la matrice d’adjacences du graphe.-
Importer le module
numpyet lui donner l’aliasnp -
Obtenir
n, la longueur du dictionnaire d’adjacences -
Obtenir
villesla liste des villes qui servent de clés dans le dictionnaire d’adjacence. -
Créer une matrice pleine de zéros nommée
matriceà l’aide de la méthodezeros()denumpy(https://numpy.org/doc/stable/reference/generated/numpy.zeros.html) -
Parcourir les lignes et les colonnes de la matrice :
-
Pour la ligne
lde la matrice :-
Afficher la ville d’indice
ldans la listevilles -
Afficher la liste des voisins de la ville d’indice
ldans la listevilles -
Pour la colonne
cde la matrice :-
Afficher la ville d’indice
cdans la listevilles -
Si la ville d’indice
cdans la listevillesest dans la liste des voisins de la ville d’indiceldans la listevilles: -
Afficher
"OK" -
Mettre la case
[l,c]de la matrice à 1
-
-
-
-
Retourner la matrice
-
-
Afficher la matrice d’adjacence du graphe
graphe_des_routes
6. Parcours de Graphes
6.1. Introduction
Le parcours d’un graphe sert à déterminer certaines de ses propriétés et caractéristiques :
-
ses connexités (tous les sommets du graphe sont joignables),
-
existence d’un circuit ou d’un cycle,
-
calcul des plus courts chemins,
-
calcul d’un arbre recouvrant,
-
algorithmes pour les flots maximums.
6.2. Chemin
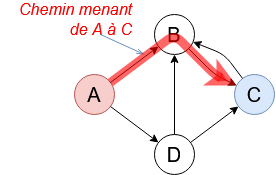
|
Un chemin est une séquence finie de sommets reliés entre eux par des arêtes. |
6.2.1. Travail à faire : Trouver le chemin
-
Donner le chemin entre les sommets A et I
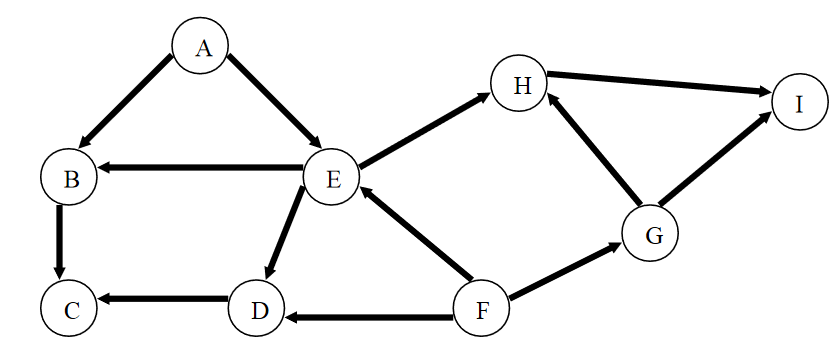
-
Existe-il un chemin entre A et F ?
6.3. Connexités
|
6.3.1. Travail à faire : graphe connexe
-
Ce graphe est-il connexe ?
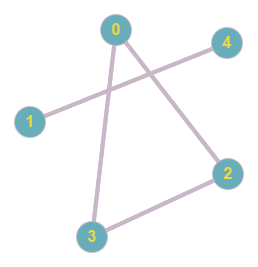
-
Quelles sont les composantes connexes de ce graphe ?
6.4. Cycles
|
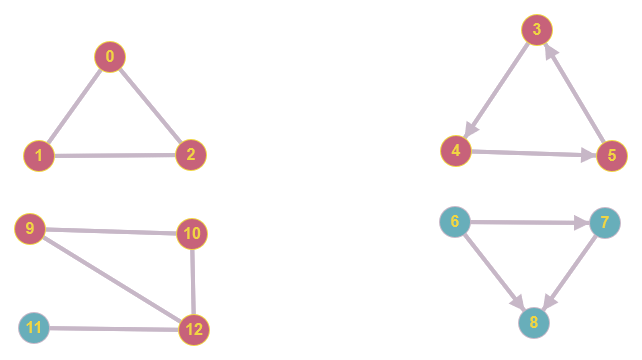
6.4.1. Travail à faire : Trouver un cycle
-
Ce graphe a-t-il un cycle ?
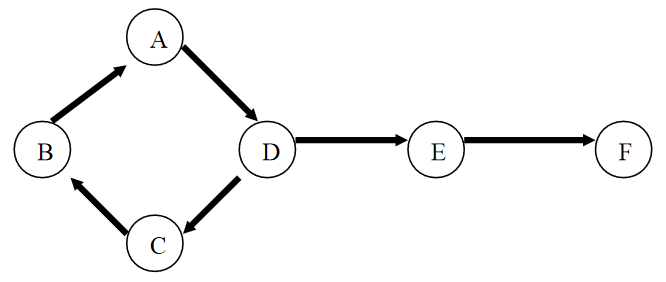
-
Ce graphe a-t-il un cycle ?

6.5. Distance
|
La distance entre deux sommets d’un graphe est la longueur (nombre d’arêtes) du chemin le plus court (s’il y en a un) reliant ces deux sommets. Si les arcs sont pondérés, on additionne les coûts de chaque arcs qui compose le chemin. |
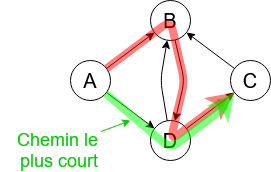
6.5.1. Travail à faire : Trouver la distance
-
Donner la distance entre les sommets A et J
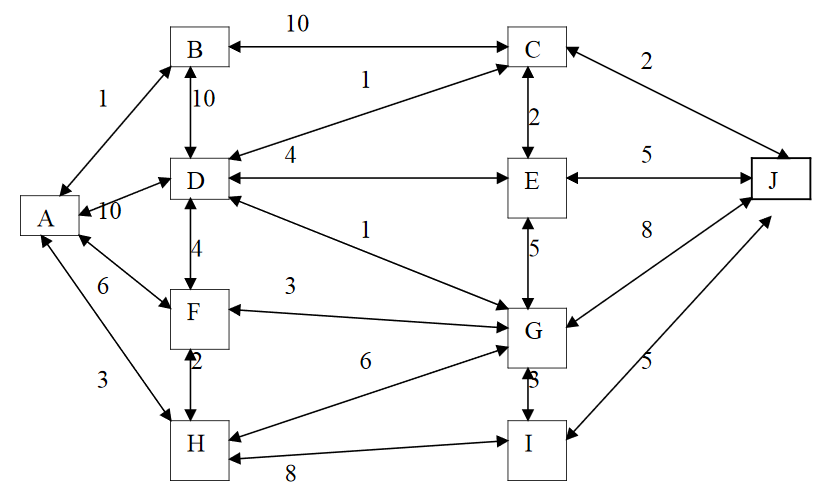
-
Donner la distance entre les sommets A et J si les arêtes ne sont pas pondérées
7. Programmation
|
Comme pour les arbres, il est possible de réaliser deux types de parcours d’un graphe :
Cependant, contrairement aux arbres :
|
7.1. Parcours en profondeur : DFS
L’exploration d’un parcours en profondeur depuis un sommet S fonctionne comme suit :
On poursuit un chemin dans le graphe jusqu’à un cul-de-sac ou alors jusqu’à atteindre un sommet déjà visité.
On revient alors sur le dernier sommet où on pouvait suivre un autre chemin puis explore un autre chemin.
L’exploration s’arrête quand tous les sommets depuis S ont été visités.
Bref, l’exploration progresse à partir d’un sommet S en s’appelant récursivement pour chaque sommet voisin de S.
7.1.1. Algorithme
PROCEDURE parcours_en_profondeur(G graph, s sommet)
marquer v comme visté
POUR TOUS les sommets voisins v de s FAIRE
SI v n'est pas marqué comme visité ALORS
APPELER RECURSIVEMENT parcours_en_prfondeur(G, v)7.1.2. Travail à faire : Codage de l’algorithme
7.2. Parcours en largeur : BFS
L’algorithme de parcours en largeur (ou BFS, pour Breadth First Search en anglais) permet le parcours d’un graphe ou d’un arbre de la manière suivante : * on commence par explorer un nœud source, * puis ses successeurs, * puis les successeurs non explorés des successeurs, etc.
L’algorithme de parcours en largeur permet de calculer les distances de tous les nœuds depuis un nœud source dans un graphe non pondéré (orienté ou non orienté).
7.2.1. Algorithme
parcours_largeur(Graphe G, Sommet s):
f = CreerFile();
f.enfiler(s);
marquer(s);
TANT QUE la file est non vide
s = f.defiler();
afficher(s);
POUR TOUT voisin t de s dans G
SI t non marqué
f.enfiler(t);
marquer(t);