Chiffrement

1. Introduction

Le chiffrement est un procédé de cryptographie grâce auquel on souhaite rendre la compréhension d’un document impossible à toute personne qui n’a pas la clé de (dé)chiffrement. Ce principe est généralement lié au principe d’accès conditionnel.

Bien que le chiffrement puisse rendre secret le sens d’un document, d’autres techniques cryptographiques sont nécessaires pour communiquer de façon sûre. Pour vérifier l’intégrité ou l’authenticité d’un document, on utilise respectivement un Message Authentication Code (MAC) ou une signature numérique. On peut aussi prendre en considération l’analyse de trafic dont la communication peut faire l’objet, puisque les motifs provenant de la présence de communications peuvent faire l’objet d’une reconnaissance de motifs. Pour rendre secrète la présence de communications, on utilise la stéganographie. La sécurité d’un système de chiffrement doit reposer sur le secret de la clé de chiffrement et non sur celui de l’algorithme. Le principe de Kerckhoffs suppose en effet que l’ennemi (ou la personne qui veut déchiffrer le message codé) connaisse l’algorithme utilisé.

https://fr.wikipedia.org/wiki/Chiffrement

— wikipédia - chiffrement

Une petite vidéo pour commencer : Introduction à la Cryptographie par l’Informateur

2. Chiffrement symétrique

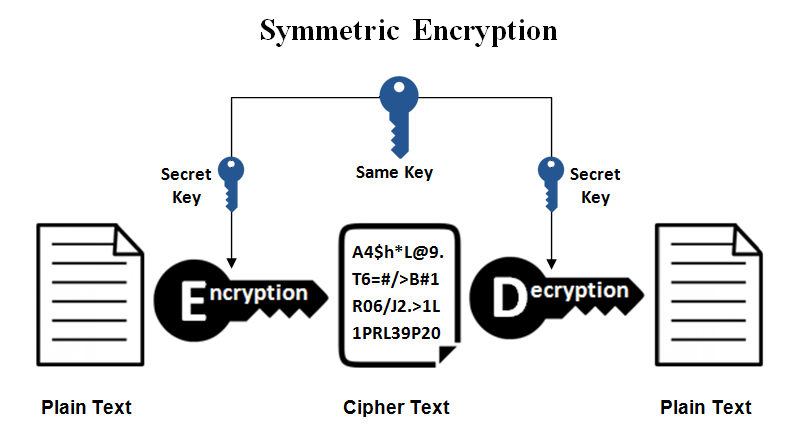
La cryptographie symétrique, également dite à clé secrète (par opposition à la cryptographie asymétrique), est la plus ancienne forme de chiffrement. Elle permet à la fois de chiffrer et de déchiffrer des messages à l’aide d’un même mot clé. On a des traces de son utilisation par les Égyptiens vers 2000 av. J.-C.

Plus proche de nous, on peut citer le chiffre de Jules César, dont le ROT13 est une variante.

https://fr.wikipedia.org/wiki/Cryptographie_symétrique

— wikipédia - chiffrement symétrique

Cette technique repose sur l’utilisation d’une clé unique qui doit être connue par l’expéditeur et le destinataire.

2.1. Le chiffrement de Cesar

La clé est un nombre entier \( n \) qui correspond à un décalage dans la table des symboles en clair.

Example 1. Application :

César utilisait un décalage de 3 lettres sur l’alphabet :

Exemple d'un chifrement Cesar par décalage de trois lettres.

Ainsi : CESAR devient FHVDU

Si on connait le décalage, on déchiffre le message en réalisant le décalage opposé, -3 lettres dans note exemple.

Si on utilise 26 lettres majuscules, il n’existe que 26 clés possibles!

2.1.2. Travail à faire : chiffrer le message en clair

2.1.3. Travail à faire : Codage de la fonction `cesar()`

Complétez le code de la fonction cesar(n,plaintext) qui chiffre ou déchiffre un message en clair plaintext avec la clé n.

Rappel :

chr(i) : Renvoie la chaîne représentant un caractère dont le code de caractère Unicode est le nombre entier i. Par exemple, chr(97) renvoie le caractère 'a'.
Les codes UTF-8 et ASCII sont identiques : table ASCII
liste.index(element) : renvoie l’indice de l’élément element dans la liste liste.

# table des symboles en clair : lettres majuscules de l'alphabet
symbol_table = [chr(i) for i in range(?, ?)]

def cesar(n,plaintext):
  # longueur de la table des symboles en clair
	l = ?
	print(f"table des {l} symboles : {symbol_table}")

  # message chiffré vide au commencement
	ciphertext =  ?

  # Pour chaque symbole dans le message à chiffrer
	for ? in ?:
    # Si le symbole est dans la table des symboles en clair
		if ? in ?:
      # Ajouter au message chiffré le symbole chiffré avec la clé n
			?
		else:
      # Ajouter au message chiffré le symbole en clair
			ciphertext += ?

  # Retourner le message chiffré
	return ciphertext

2.2. Chiffrement de Vigenère

Le chiffre de Vigenère est un système de chiffrement par substitution polyalphabétique dans lequel une même lettre du message clair peut, suivant sa position dans celui-ci, être remplacée par des lettres différentes, contrairement à un système de chiffrement mono alphabétique comme le chiffre de César (qu’il utilise cependant comme composant). Cette méthode résiste ainsi à l’analyse de fréquences, ce qui est un avantage décisif sur les chiffrements mono alphabétiques. Cependant le chiffre de Vigenère a été percé par le major prussien Friedrich Kasiski qui a publié sa méthode en 1863. Depuis cette époque, il n‘offre plus aucune sécurité.

Il est nommé ainsi au XIXe siècle en référence au diplomate du XVIe siècle Blaise de Vigenère, qui le décrit (intégré à un chiffrement plus complexe) dans son traité des chiffres paru en 1586. On trouve en fait déjà une méthode de chiffrement analogue dans un court traité de Giovan Battista Bellaso paru en 1553.

https://fr.wikipedia.org/wiki/Chiffre_de_Vigenère

— wikipédia - chiffre de Vigenère

Cette méthode a été mise au point durant la renaissance pour contrer la cryptanalyse par la méthode des fréquences de lettres qui permettait de "casser" les clés de cryptage assez facilement.

On choisit une clé sous la forme d’un mot ou d’une phrase qui donne le décalage à appliquer qui devient alors variable.

Supposons que la clé soit ABC, les décalages successifs seront 0, 1, 2, 0, 1, 2, 0, …

Example 2. Application :

Clé de chiffrement : CLE Message en clair : VIGENERE Table de symboles en clair : ABCDEFGHIJKLMNOPQRSTUVWXYZ

V est chiffré avec la clé C selon le chiffrement de Cesar :
V est décalé de 2 → X
I est chiffré avec la clé L selon le chiffrement de Cesar :
I est décalé de 11 → T
G est chiffré avec la clé E selon le chiffrement de Cesar :
G est décalé de 4 → K
E est chiffré avec la clé C selon le chiffrement de Cesar :
E est décalé de 2 → G
N est chiffré avec la clé L selon le chiffrement de Cesar :
N est décalé de 11 → Y
E est chiffré avec la clé E selon le chiffrement de Cesar :
E est décalé de 4 → I
R est chiffré avec la clé C selon le chiffrement de Cesar :
R est décalé de 2 → T
E est chiffré avec la clé L selon le chiffrement de Cesar :
E est décalé de 11 → P

Message chiffré : XTKGYITP

Pour chiffrer un message selon le chifremment de Vigenère, on peut utiliser une table de correspondance. On parle de Code de Vignère

2.2.1. Travail à faire : Coder un message en clair

Codez le message suivant selon le principe du chiffrement de Vigenère :

Clé : NSI
Message en clair : BONJOUR LE MONDE
Table des symboles : ABCDEFGHIJKLMNOPQRSTUVWXYZ
Tout symbole qui n’est pas dans la table est conservé

Correction

OGVWGCE DM ZGVQW

2.2.2. Travail à faire : Décoder un message codé

Décodez le message suivant selon le principe du chiffrement de Vigenère :

Clé : NSI
Message chiffré : W’SCESQ ZGV OSK!
Table des symboles : ABCDEFGHIJKLMNOPQRSTUVWXYZ
Tout symbole qui n’est pas dans la table est conservé

Correction

J’AURAI MON BAC!

2.2.3. Travail à faire :Codage d’une fonction de chiffrement de Vigenère

A l’aide de la fonction cesar(n,plaintext), écrivez une fonction encrypt_vigenere(key,plaintext) qui chiffre le message en clair plaintext en utilisant la clé key. La table des symboles est composée des lettres majuscules de l’alphabet et tout symbole qui n’appartient pas à la table est conservé.

Correction

Exemple de solution

def encrypt_vigenere(key, plaintext):
	ciphertext = ""
	i = 0
	for symbol in plaintext:
		if symbol in symbol_table:
			cesar_key = symbol_table.index(key[i%len(key)])
			i += 1
			encrypt_symbol = cesar(cesar_key,symbol)
			print(symbol, "\t", key[i%len(key)], "\t", cesar_key, "\t", encrypt_symbol)
			ciphertext += encrypt_symbol
		else:
			ciphertext += symbol
	return ciphertext

print(encrypt_vigenere('NSI','BONJOUR LE MONDE'))

2.2.4. Travail à faire :Codage d’une fonction de déchiffrement de Vigenère

A l’aide de la fonction cesar(n,plaintext), écrivez une fonction decrypt_vigenere(key,ciphertext) qui déchiffre le message chiffré ciphertext en utilisant la clé key. La table des symboles est composée des lettres majuscules de l’alphabet et tout symbole qui n’appartient pas à la table est conservé.

Correction

Exemple de solution

def decrypt_vigenere(key, ciphertext):
	plaintext = ""
	i = 0
	for symbol in ciphertext:
		if symbol in symbol_table:
			cesar_key = symbol_table.index(key[i%len(key)])
			i += 1
			decrypt_symbol = cesar(-cesar_key,symbol)
			print(symbol, "\t", key[i%len(key)], "\t", cesar_key, "\t", decrypt_symbol)

			plaintext += decrypt_symbol
		else:
			plaintext += symbol
	return plaintext

print(decrypt_vigenere('NSI', 'OGVWGCE DM ZGVQW'))

2.2.5. Travail à faire :On s’amuse (un peu !)

Utilisez votre serveur Discord pour envoyer des messages chiffrés.

Quel préalable est nécessaire pour que les participants soient certains de la confidentialité des échanges ?

Correction

La connaissance de la clé doit être limitée aux seuls particiants aux échanges.

2.3. Utilisation de la fonction XOR

Le chiffrement et le déchiffrement de messages à partir d’une même clé peut être fait en utilisant la fonction logique XOR.

Rappel :

\( S = a \oplus b ⇒ a = S \oplus b \)

2.3.1. Travail à faire :Démonstration

Complétez les tables de vérité des expressions suivante et démontrez que la relation précédente est vraie.

Correction

En conclusion :

Si on note \(M\) le message et \(S\) la clé secrète, alors on obtient le message chiffré \(C\) faisant :

\[\LARGE{C = M \oplus S}\]

Le déchiffrement se fait tout simplement en appliquant la même opération :

\[\LARGE{M = C \oplus S}\]

2.3.2. Travail à faire :Application

A l’aide de la table ASCII, codez le message suivant en clair :

plaintext = "NSI"

La clé de chiffrement est :

secret_key = 0b0011 1010

Quel sera le message chiffré en binaire ?

A l’aide de la table ASCII, décodez le message chiffré :

ciphertext = 0b01110100 0b01101001 0b01110011

La clé de chiffrement est :

secret_key = ":"

Quel était le message en clair (caractères) ?

2.3.3. Travail à faire :Codage d’une fonction de chiffrement XOR

Ecrivez une fonction encrypt_xor(key,plaintext) qui chiffre le message en clair plaintext en utilisant la clé key :

plaintext : chaine de caractères à chiffrer
key : clé de chiffrement limitée à un seul caractère (8 bits)

Rappel :

chr(i) : Renvoie la chaîne représentant un caractère dont le code de caractère Unicode est le nombre entier i. Par exemple, chr(97) renvoie le caractère 'a'.
ord(car) : Renvoie le code ASCII du caractère car. Par exemple, ord('a') renvoie le nombre 97.
bin(number) : Renvoie la représentation binaire du nombre entier number. Par exemple, bin(97) renvoie '0b01100001'.
En python, l’opérateur logique bit à bit XOR est matérialisé par le caractère ^. Par exemple, a ^ b retourne le résultat de l’opération bit à bit \(a \oplus b \).

Votre fonction doit afficher le message chiffrer en binaire pendant le chiffrement et renvoyer la chaine chiffrer :

print(encrypt_xor(':','NSI'))

N : 0b1001110
S : 0b1010011
I : 0b1001001
tis

Correction

Exemple de solution

def encrypt_xor(key, plaintext):
	ciphertext = ""
	for car in plaintext:
		print(car, ":", bin(ord(car)))
		ciphertext += chr(ord(car) ^ ord(key))
	return ciphertext

print(encrypt_xor(':','NSI'))

2.3.4. Travail à faire :Codage d’une fonction de déchiffrement XOR

Ecrivez une fonction decrypt_xor(key,ciphertext) qui déchiffre le message chiffré ciphertext en utilisant la clé key :

ciphertext : chaine de caractères à déchiffrer (attention, certains caractères ASCII ne sont pas imprimables, mais possède bien une représentation binaire distincte !)
key : clé de chiffrement limitée à un seul caractère (8 bits)

Rappel :

chr(i) : Renvoie la chaîne représentant un caractère dont le code de caractère Unicode est le nombre entier i. Par exemple, chr(97) renvoie le caractère 'a'.
ord(car) : Renvoie le code ASCII du caractère car. Par exemple, ord('a') renvoie le nombre 97.
bin(number) : Renvoie la représentation binaire du nombre entier number. Par exemple, bin(97) renvoie '0b01100001'.
En python, l’opérateur logique bit à bit XOR est matérialisé par le caractère ^. Par exemple, a ^ b retourne le résultat de l’opération bit à bit \(a \oplus b \).

Votre fonction doit afficher le message chiffrer en binaire pendant le chiffrement et renvoyer la chaine chiffrer :

print(decrypt_xor(':','tis'))

t : 0b1110100
i : 0b1101001
s : 0b1110011
NSI

Correction

Exemple de solution

def decrypt_xor(key, ciphertext):
	plaintext = ""
	for car in ciphertext:
		print(car, ":", bin(ord(car)))
		plaintext += chr(ord(car) ^ ord(key))
	return plaintext

ciphertext = encrypt_xor('?','Salut !')
print(decrypt_xor('?',ciphertext))

2.4. Conclusion chiffrement symétrique

Repose sur l’untilisation d’une clé unique connue de l’émetteur et du destinataire.
Le principal avantage du chiffrement symétrique est qu’il est facile à réaliser.
L’inconvénient est que la clé secrète doit être partagée avec le destinataire. Si quelqu’un apprend cette clé secrète, tous les messages chiffrés sont compromis.

3. Chiffrement asymétrique

La cryptographie asymétrique, ou cryptographie à clef publique est un domaine relativement récent de la cryptographie. Elle permet d’assurer la confidentialité d’une communication, ou d’authentifier les participants, sans que cela repose sur une donnée secrète partagée entre ceux-ci, contrairement à la cryptographie symétrique qui nécessite ce secret partagé préalable.

La cryptographie asymétrique peut être illustrée avec l’exemple du chiffrement à clef publique et privée, dont le but, comme tout chiffrement, est de garantir la confidentialité d’une donnée lors d’une transmission de celle-ci.

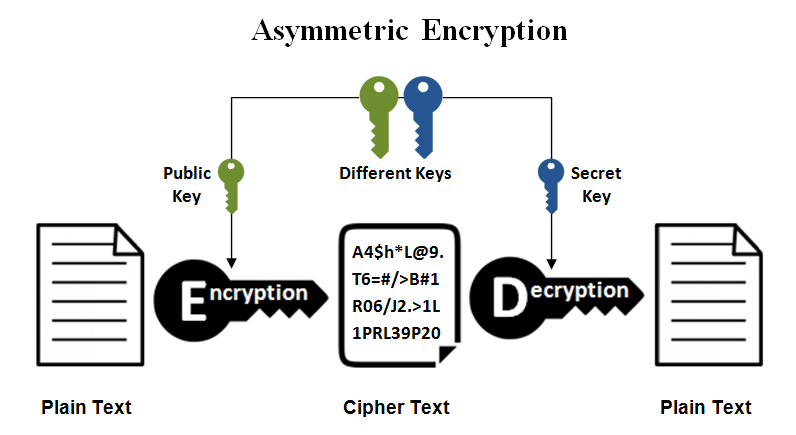
Le terme asymétrique s’explique par le fait qu’il utilise deux clefs différentes,

l’une, la clef publique, pour chiffrer,

l’autre, la clef privée, pour déchiffrer.

L’utilisateur qui souhaite recevoir des messages engendre un tel couple de clefs. Il ne transmet à personne la clef privée alors que la clef publique est transmissible sans restriction2. Quiconque souhaite lui envoyer un message confidentiel utilise la clef publique pour chiffrer celui-ci. Le message chiffré obtenu ne peut être déchiffré que connaissant la clef privée. Il peut donc être communiqué publiquement : la confidentialité du message original est garantie. Le destinataire, qui n’a communiqué à personne sa clef privée, est le seul à pouvoir, à l’aide de celle-ci, déchiffrer le message transmis pour reconstituer le message original.

https://fr.wikipedia.org/wiki/Cryptographie_asymétrique

— wikipédia - chiffrement asymétrique

La cryptographie asymétrique permet de résoudre le problème de l’échange d’une clé secrète.

Elle a été inventée par Whitfield Diffie et Martin Hellman en 1976, qui reçurent le prix Turing de 2015 pour cette découverte.

Pour assurer un asymétrique on dispose de 2 clés :

la clé publique : tout le monde peut la posséder, il n’y a aucun risque à la la transmettre. Elle sert à chiffrer le message.
la clé privée : seul le destinataire la possède. Elle sert à déchiffrer le message chiffré.

3.1. Principe

Pour que cela fonctionne, il faut que la paire clé publique/clé privée ait une propriété particulière.

Soit \( F_P \) la fonction de chiffrement utilisée avec la clé publique, et \( F_S \) la fonction relative à la clé privée. Une relation particulière relie ces deux fonctions:

\[\large{ m=F_S(F_P(m)) }\]

Enfin pour que ce système fonctionne, il faut que:

la fonction \( F_P \) soit facile à calculer pour tout le monde,
la fonction \( F_S \) soit facile à calculer uniquement pour le détenteur de la clé privée.

Un système qui satisfait ces deux critères est le système de chiffrement RSA utilisé pour échanger des données confidentielles sur Internet.

Cet algorithme fut inventé en 1977 par Ronald Rivest, Adi Shamir et Leonard Adleman (initiales RSA) breveté par le MIT en 1983. Le brevet a expiré le 21 septembre 2000 ce qui permet de l’utiliser librement depuis.

3.2. Algorithme RSA

Ce système de cryptographie repose sur l’utilisation de nombres premiers et certaines propriétés de l’arithmétique modulaire.

Alice et Bob souhaitent échanger des données secrètes. Eve (la méchante sur internet !) cherche à casser le code.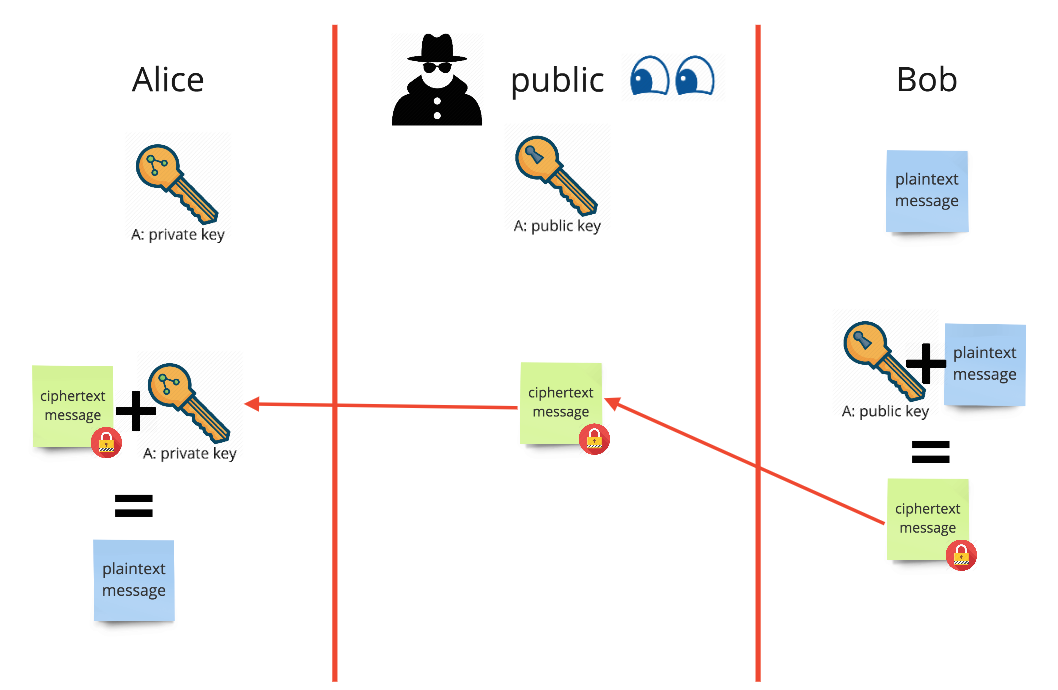

Disons que Bob veut envoyer à Alice un message simplement constitué de la lettre "B". Alice doit générer une paire de clés, fournir à Bob sa clé publique et conserver sa clé privée.

Chaque clé peut être représentée par les couples \((e, n), (d, n)\) où \(e,d,n\) sont obtenus selon l’algorithme suivant :

Choisir \(p\) et \(q\), deux nombres premiers distincts ;
calculer leur produit \(n = p \times q\), appelé module de chiffrement ;
calculer \(\varphi (n) = (p - 1)(q - 1)\)
choisir un entier naturel \(e\) premier avec \(\varphi (n)\) tel que \(e < \varphi (n)\), appelé exposant de chiffrement ;
calculer l’entier naturel \(d\), inverse modulaire de \(e\) pour la multiplication \(mod[\varphi (n)]\), appelé exposant de déchiffrement ;

\[\LARGE{e \times d \equiv 1 \quad mod[\varphi (n)] \Leftrightarrow (e \times d) \space \% \space \varphi (n) = 1 }\]

Chiffrer un message en clair \( M \) pour obtenir un message chiffré \( C \) :
- Clé publique : \(\large{(e,n)}\)
- Chiffrement : \(\large{C = M^e \space \% \space n}\)
déchiffrer un message chiffré \( M \) pour obtenir un message chiffré \( C \) :
- Clé privée : \(\large{(d,n)}\)
- Déchiffrement : \(\large{M = C^d \space \% \space n}\)

Example 3. Chiffrement et déchiffrement

Alice génère une paire de clés :

On choisi aléatoirement \(p=2\) et \(q=7\) (remarque: on prend ici des nombres petits pour faciliter les calculs)
\( n=2 \times 7 = 14\)
\( \varphi (n)=(2-1)(7-1) = 6\)
On choisi \( e \) tel que \( 1 < e < 6 \) et \(e\) est premier avec \(6\), c’est à dire \( pgcd(e,6) = 1 \)
- On a le choix entre \( 2,3,4,5\)
- Seul \(5\) convient
On choisi \(d\) tel que \((5 \times d) \% \space 6 = 1 \)
- On cherche le nombre \(d\) tel que \( 5 \times d - 1 \) est un multiple de \(6\)
- Soit \(6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …\)
- On remarque que \(5 \times 11 - 1 = 54 \)
- donc \(d=11\) convient

Clé publique : \(\large{(5,14)}\) diffusée publiquement et donc accessible par Bob et la méchante Eve.
Clé privée : \(\large{(11,14)}\) conservée secrète par Alice
Remarques :
- le module de chiffrement est \(14\), on ne peut donc chiffrer que les codes \(0\) à \(13\)
- Eve pourrait se faire passer pour Bob pour envoyer des messages à Alice, mais ne peut pas déchiffrer les message envoyé par Bob à Alice.

\(M ="B"\) disons que le code de "B" est \(2\) donc \(M =2\)
Chiffrement : \(\large{C = 2^5 \space \% \space 14 = 4 }\)
Déchiffrement : \(\large{M = 4^{11} \space \% \space 14 = 2}\)
On retrouve bien \(2\) soit le code du caractère "B" transmis par Alice

3.2.1. Travail à faire :Recherche du pgcd

L’algorithme RSA de génération des clés nécessite le calcul du PGCD de deux nombres. Commençons par nous doter d’une fonction pgcd(n,m) qui retourne le plus grand diviseur commun de deux nombres entiers n et m.

Définition

Pour tout entier naturel \(a\) :

\[\LARGE{PGCD(a,0) = a}\]

Soit \(a\) et \(b\) deux entiers naturels différents de zéro et \(r\) le reste de la division de \(a\) par \(b\) :

\[\LARGE{PGCD(a,b) = PGCD(b,r)}\]

Codez la fonction pgcd(n,m) qui retourne le plus grand diviseur commun de deux nombres entiers n et m.

Correction

Exemple de solution

def pgcd(m,n):
    if n==0:
        return m
    else:
        return pgcd(n,m%n)

n,m = 60, 48
print(f"Le PGCD de {n} et {m} est {pgcd(n,m)}")

n,m = 60, 47
print(f"Le PGCD de {n} et {m} est {pgcd(n,m)}")

3.2.2. Travail à faire :Fonction de génération des clés

Cette fonction doit permettre de générer la pair de clés publique et privée qui servirons respectivement au chiffrement et au déchiffrement.

Complétez la fonction generate_keys(p,q) qui retourne une liste contenant une paire de clés à partir de deux nombres premiers p et q :
Testez votre fonction pour p=29 et q=31. Vous devriez obtenir la sortie suivante :

p = 29
q = 31
p=29 et q=31
clé publique : (11, 899)
clé privée :  (611, 899)

def generate_keys(p,q):
  # calcul de n
	n = ?

  # calcul de phi(n)
	phi = ?

  #calcul de e
	e=2
	while e<? and pgcd(?)!= ?:
	    e+=1

  # calcul de d
  d = 1
	while ?:
	    d +=1

  # retourne la clé publique et la clé privée (dans cet ordre !)
  return [(e,n),(d,n)]

p = int(input("p = "))
q = int(input("q = "))

keys = generate_keys(p,q)

public_key = keys[0]
private_key = keys[1]

print("clé publique :", public_key)
print("clé privée : ", private_key)

Correction

Exemple de solution

def generate_keys(p,q):
  # calcul de n
	n = p*q

  # calcul de phi(n)
	phi = (p-1)*(q-1)

  #calcul de e
	e=2
	while e<phi and pgcd(e,phi)!= 1:
	    e+=1

  # calcul de d
  d = 1
	while (e*d - 1) % phi != 0:
	    d +=1

  # retourne la clé publique et la clé privée (dans cet ordre !)
  return [(e,n),(d,n)]

3.2.3. Travail à faire :Fonction de chiffrement RSA

Cette fonction doit permettre de chiffrer un message en clair à l’aide de la clé publique.

Complétez la fonction encrypt_rsa(public_key, plaintext) qui retourne le message en clair plaintext chiffré à l’aide de la clé public_key :
Avec les clés générées précédemment, chiffrez le message 'Salut tout le monde !', vous devriez obtenir :

on chiffre 'Salut tout le monde ! : 'Æͨɻ˳tÚt˥˳tÚÚ˸˥ͺÚǲ'

def encrypt_rsa(public_key, plaintext):
  #public_key est un tuple : (e,n)
	e = ?
	n = ?

  # texte chiffré, ne contient rien au commencement
	ciphertext = ?

  # Pour chaque caractère dans le message en clair
	for car in ?:
    # on ajoute au message chiffré le caractère chiffré : C = M**e % n
    # On travail sur le code uncode du caractère : chr() et ord()
		ciphertext += ?

  # retourne le message chiffré
	return ciphertext

Correction

Exemple de solution

def encrypt_rsa(public_key, plaintext):
	e = public_key[0]
	n = public_key[1]
	ciphertext = ""
	for car in plaintext:
		ciphertext += chr(ord(car)**e % n)
	return ciphertext

message_clair = "Salut tout le monde !"
message_chiffre = encrypt_rsa(public_key, message_clair)
print(f"on chiffre '{message_clair} : '{message_chiffre}'")

3.2.4. Travail à faire :Fonction de déchiffrement RSA

Cette fonction doit permettre de chiffrer un message en clair à l’aide de la clé publique.

Codez la fonction decrypt_rsa(privat_key, ciphertext) qui retourne le message chiffré ciphertext déchiffré à l’aide de la clé private_key.
Dechiffrez le message précédemment chiffré et vérifiez qu’il est fidèlement restitué.

Remarque : Aidez vous de la fonction précédente encrypt_rsa() et de la définition du déchiffrifrement RSA : \(M = C^d \space \% \space n\)

Correction

Exemple de solution

def decrypt_rsa(private_key, ciphertext):
	d = private_key[0]
	n = private_key[1]
	plaintext = ""
	for car in ciphertext:
		plaintext += chr(ord(car)**d % n)
	return plaintext

message_clair = "Salut tout le monde !"
message_chiffre = encrypt_rsa(public_key, message_clair)
print(f"on chiffre '{message_clair} : '{message_chiffre}'")
message_clair = decrypt_rsa(private_key, message_chiffre)
print(f"on déchiffre '{message_chiffre}' : '{message_clair}'")

3.2.5. Travail à faire :Attaque par brute force

Une attaque par brute force consiste à tester des clés de déchiffrement jusqu’à ce qu’on trouve la bonne, c’est à dire jusqu’à ce que le message à déchiffrer apparaisse en clair.

Dans le cas de RSA, cette technique consiste à trouver le paramètre \(d\) de la clé privée connaissant le paramètre \(n\). Le travail est simplifié si on connait une partie du message à déchiffrer.

Complétez la fonction brute_force(n, list_cipher_char, contain) qui retourne la clé privée de déchiffrement RSA connaissant le paramètre n qui est connue grace à la clé publique, un message chiffré à l’aide de la clé à casser et une partie du message d’origine en clair (connue ou supposée) contain.
Si au terme de 10000 tentatives la clé n’est pas trouvée, la fonction retourne False.

Remarque : Alan Turing a utiliser cette technique qu’on appelle indice de coïncidence pour rechercher un motif connue dans les messages allemands cryptés avec Enigma

La méthode de l’indice de coïncidence a notamment été utilisée pour décrypter une expression qui revenait souvent en fin de message chiffré et qui s’est révélée être « HEIL HITLER », …

https://fr.wikipedia.org/wiki/Cryptanalyse_d’Enigma

— wikipédia - Cryptanalyse d'Enigma

Cassez la clé de déchiffrement sachant que :
- clé publique : (1903, 2117)
- Le message en clair contient NSI
- message chiffré :

['0x812', '0x171', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x3e1', '0x156', '0xe9', '0x83', '0x6e7', '0x5cc', '0x370', '0x582', '0x171', '0x1fb', '0x6e7', '0x370', '0x78b', '0x6e7', '0x370', '0x3de', '0x6e7', '0x4a4', '0x4a4', '0x709', '0x771', '0x6e7', '0x17b', '0x370', '0x78b', '0x199', '0x6e7', '0x4a4', '0x3f7', '0x370', '0x49b', '0xe9', '0x6e7', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x709', '0x83', '0x6e7', '0x5cc', '0x370', '0x3de', '0x6e7', '0x3d5', '0x6e7', '0x1fb', '0x370', '0x2f', '0x370', '0x212', '0x171', '0x6e7', '0x3d5', '0x370', '0x83', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3de', '0x171', '0x4a4', '0x4a4', '0x171', '0x156', '0x3d5', '0x817', '0x5ca', '0x7ff', '0x197', '0x582', '0x171', '0x78b', '0x171', '0x3f7', '0x709', '0x3f7', '0x171', '0x156', '0x3d5', '0x370', '0x23d', '0x23d', '0x23d', '0x5ca', '0x4fb', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3e1', '0x1fb', '0x156', '0xcd', '0x6e7', '0x4a4', '0x4a4', '0x6e7', '0xe9', '0x1fb', '0x370', '0x3e3', '0x6e7', '0x370', '0x750', '0x812', '0x124']

Remarque : Le message chiffré est constitué des codes unicode de chaque caractère en hexadécimal car certains caratères ne sont pas imprimables. Il faut donc apporter certaines modifications à la fonction de déchiffrement pour qu’elle prenne en paramètre la liste des codes unicode des caratères du message chiffré et non plus une chaine de caractères comme nous l’avions fait précédemment :

def decrypt_rsa(private_key, list_cipher_char):
	d = private_key[0]
	n = private_key[1]
	plaintext = ""
	for car in list_cipher_char:
		plaintext += chr(int(car,16)**d % n)
	return plaintext

# Partie à compléter

def brute_force(n, list_cipher_char, contain):
	plaintext = ""
	d = 1
  # tant que le motif rechercé (contain) n'apparait pas dans le message déchiffré
	while ?:
    # limite à 10000 tentatives avant de retourner False
		if ?:
			return ?
		d+=1
    # on tente de déchiffrer la liste des caractères du message chiffré avec la clé à tester
		plaintext = ?

		print(f"clé : {(d,n)} => '{plaintext}'")
  # ça a marché ! on retourne la clé trouvée sous forme d'un tuple
	return ?

public_key = (1903, 2117)
message_chiffre_hex = ['0x812', '0x171', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x3e1', '0x156', '0xe9', '0x83', '0x6e7', '0x5cc', '0x370', '0x582', '0x171', '0x1fb', '0x6e7', '0x370', '0x78b', '0x6e7', '0x370', '0x3de', '0x6e7', '0x4a4', '0x4a4', '0x709', '0x771', '0x6e7', '0x17b', '0x370', '0x78b', '0x199', '0x6e7', '0x4a4', '0x3f7', '0x370', '0x49b', '0xe9', '0x6e7', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x709', '0x83', '0x6e7', '0x5cc', '0x370', '0x3de', '0x6e7', '0x3d5', '0x6e7', '0x1fb', '0x370', '0x2f', '0x370', '0x212', '0x171', '0x6e7', '0x3d5', '0x370', '0x83', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3de', '0x171', '0x4a4', '0x4a4', '0x171', '0x156', '0x3d5', '0x817', '0x5ca', '0x7ff', '0x197', '0x582', '0x171', '0x78b', '0x171', '0x3f7', '0x709', '0x3f7', '0x171', '0x156', '0x3d5', '0x370', '0x23d', '0x23d', '0x23d', '0x5ca', '0x4fb', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3e1', '0x1fb', '0x156', '0xcd', '0x6e7', '0x4a4', '0x4a4', '0x6e7', '0xe9', '0x1fb', '0x370', '0x3e3', '0x6e7', '0x370', '0x750', '0x812', '0x124']

private_key = brute_force(public_key[1], message_chiffre_hex, 'NSI')
if private_key:
	print(f"Clé cassée : {private_key}")
else:
	print("Pas réussi à casser la clé")

Correction

Exemple de solution

def brute_force(n, list_cipher_char, contain):
	plaintext = ""
	d = 1
  # tant que le motif rechercé (contain) n'apparait pas dans le message déchiffré
	while contain not in plaintext:
    # limite à 10000 tentatives avant de retourner False
		if d>10000:
			return False
		d+=1
    # on tente de déchiffrer la liste des caractères du message chiffré avec la clé à tester
		plaintext = decrypt_rsa((d,n),list_cipher_char)

		print(f"clé : {(d,n)} => '{plaintext}'")
  # ça a marché ! on retourne la clé trouvée sous forme d'un tuple
	return (d,n)

3.3. Conclusion RSA

Des valeurs modestes de \(p\) et \(q\) peuvent évidemment facilement être retrouvées, c’est pourquoi la cryptographie RSA actuelle est basée sur des nombres premiers gigantesques qui peuvent être composés de plus de 200 chiffres !

Ainsi, imaginé en 1977, le RSA résiste encore aujourd’hui aux attaques5 et est couramment utilisé dans les échanges internet et/ou commerciaux.

Chiffrement

1. Introduction

2. Chiffrement symétrique

2.1. Le chiffrement de Cesar

2.1.1. Travail à faire : déchiffrer le message chiffré

2.1.2. Travail à faire : chiffrer le message en clair

2.1.3. Travail à faire : Codage de la fonction `cesar()`

2.2. Chiffrement de Vigenère

2.2.1. Travail à faire : Coder un message en clair

2.2.2. Travail à faire : Décoder un message codé

2.2.3. Travail à faire :Codage d’une fonction de chiffrement de Vigenère

2.2.4. Travail à faire :Codage d’une fonction de déchiffrement de Vigenère

2.2.5. Travail à faire :On s’amuse (un peu !)

2.3. Utilisation de la fonction XOR

2.3.1. Travail à faire :Démonstration

2.3.2. Travail à faire :Application

2.3.3. Travail à faire :Codage d’une fonction de chiffrement XOR

2.3.4. Travail à faire :Codage d’une fonction de déchiffrement XOR

2.4. Conclusion chiffrement symétrique

3. Chiffrement asymétrique

3.1. Principe

3.2. Algorithme RSA

3.2.1. Travail à faire :Recherche du pgcd

3.2.2. Travail à faire :Fonction de génération des clés

3.2.3. Travail à faire :Fonction de chiffrement RSA

3.2.4. Travail à faire :Fonction de déchiffrement RSA

3.2.5. Travail à faire :Attaque par brute force

3.3. Conclusion RSA

4. Sources

\(a\)	\(b\)	\(S = a \oplus b\)		\(S \oplus b\)
0	0
0	1
1	0
1	1

Chiffrement

1. Introduction

2. Chiffrement symétrique

2.1. Le chiffrement de Cesar

2.1.1. Travail à faire : déchiffrer le message chiffré

2.1.2. Travail à faire : chiffrer le message en clair

2.1.3. Travail à faire : Codage de la fonction cesar()

2.2. Chiffrement de Vigenère

2.2.1. Travail à faire : Coder un message en clair

2.2.2. Travail à faire : Décoder un message codé

2.2.3. Travail à faire :Codage d’une fonction de chiffrement de Vigenère

2.2.4. Travail à faire :Codage d’une fonction de déchiffrement de Vigenère

2.2.5. Travail à faire :On s’amuse (un peu !)

2.3. Utilisation de la fonction XOR

2.3.1. Travail à faire :Démonstration

2.3.2. Travail à faire :Application

2.3.3. Travail à faire :Codage d’une fonction de chiffrement XOR

2.3.4. Travail à faire :Codage d’une fonction de déchiffrement XOR

2.4. Conclusion chiffrement symétrique

3. Chiffrement asymétrique

3.1. Principe

3.2. Algorithme RSA

3.2.1. Travail à faire :Recherche du pgcd

3.2.2. Travail à faire :Fonction de génération des clés

3.2.3. Travail à faire :Fonction de chiffrement RSA

3.2.4. Travail à faire :Fonction de déchiffrement RSA

3.2.5. Travail à faire :Attaque par brute force

3.3. Conclusion RSA

4. Sources

2.1.3. Travail à faire : Codage de la fonction `cesar()`